Mała całeczka samotna jak świat Zuzik Piskorz:

	1+√x+x2+x
∫		dx
	x2

iks:

	1
∫(x−2 + x−3/2 + 1 +		)dx
	x

Artur z miasta Neptuna: podałem wynik gdzieś tam wcześniej

Zuzik Piskorz: Artur : umiesz wyznaczać asymptoty

Artur z miasta Neptuna: umiem

Zuzik Piskorz: a pomożsesz?

	x2−3
) ekstrema i asymptoty dla : y= xe−x i y=
	x−2

	−1
i asymptoty pi≠onowe i poziome dla :		dla x≠ −3
	ex+3

0 dla x=−3 I to jest układ

Artur z miasta Neptuna: zacznę od tego drugiego −−− pionowej nie ma bo D_f = R poziome −−− oblicz granicę w '+' i '−' ∞ (wyjdzie odpowiednio '0' i −∞) więc w +∞ masz poziomą y=0, w −∞ musisz obliczyć ukośną (jeżeli to wynika z treści zadania, jeżeli nie to piszesz że brak poziomej dla '−∞')

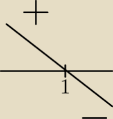
Artur z miasta Neptuna: pierwsze y=xe^−x asymptoty pionowe nie ma (D_f =R) asymptoty poziome (granice w '+' i '−' ∞ wychodzą odpowiednio '0' i '−∞') asymptota ukośna dla '−∞' lim (f(x)/x) = lim e^−x = 0 lim (f(x) − ax) = lim fx = −∞ czyli brak ukośnej f' = e^−x − x*e^−x = e^−x(1−x) f' = 0 ⇔ 1−x = 0 ⇔ x=1 rysuję 'rysunek' (schemat wykresu pochodnej funkcji) i wniosek: f posiada ekstremum lokalne x₀ = 1 i jest to maksimum lokalne f↗ w (−∞,1) f↘ w (1, ∞)

Zuzik Piskorz: a jak obliczyć w 2 w −∞

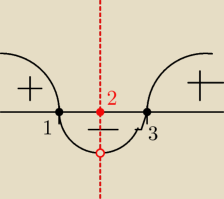
Artur z miasta Neptuna: drugie

	x2−3
y =
	x−2

D_f = R/{2} asymptota pionowa dla x=2 granice w '2⁻' i '2⁺' wychodzą (odpowiednio) '−∞' i '+∞' asymptota pozioma (granice w '+' i '−' ∞ wychodzą odpowiednio '∞' i '−∞' asymptota ukośna lim_−∞ f(x)/x = 1 lim_∞ f(x)/x = 1 lim_−∞ f(x) − x = −2 lim_−∞ f(x) − x = −2 jest ukośna dla '−∞' i '+∞' (taka sama) i wynosi y=x−2

	2x(x−2) − (x2−3)		x2 − 4x + 3)		(x−1)(x−3)
f' =		=		=
	(x−2)2		(x−2)2		(x−2)2

D_f' = D_f (x−2)² > 0 dla każdego x ∊ D_f' f' = 0 ⇔ (x−1)(x−3) rysunek ekstremum w: x₀ = 1 (maksiumum lok.) x₀ = 3 (minimum lok.) f↗ w (−∞,1), w (3, ∞) f↘ w (1, 2), w (2,3)

DZIADZIA: Artur sory że truję ale nikt nie potrafi podołać temu zadaniu! może Ty dasz radę bo może w tobie siła neptuna