. elpe: [W kwadracie ABCD dane są A=(1,0), AC^→[8,4]. Wyznacz równania prostych, w których zawarte są przekątne tego kwadratu. prosze o jakieś wytłumaczenie bo coś mi analityczna nie idzie.

Basiek : No... widzisz. C(x,y) AC[x−1,y−0]= [8,4] x= y= No i prosta AC y=ax+b (podstawiasz współrzędne x−owe i y−kowe)=> masz równanie jednej przekątnej.

	1
Druga jest prostą prostopadłą (współczynnik a'= −		) i przechodzi przez środek prostej AC
	a

(nazwijmy to punktem M) M ma współrzędne połowy współrzędnych końców. No i y=a'x+b (podstawiasz M) −> wychodzi.

Basiek : analityczna na płaszczyźnie Chyba mój ulubiony dział

ICSP: wielomiany

elpe: a ja tak tego nie cierpię ze...

Basiek : Bo trzeba mieć sporo cierpliwości i nigdzie się nie pomylić. Mnie tak zainteresowało na próbnej maturze zadanie z analitycznej, że zostawiłam wszystkie inne zad. i liczyłam to jakieś 5x aż mi wyszło dobrze. Dzięki temu znalazłam tam po oddaniu takie błędy jak wyciągnięcie x z cosinusa przed nawias Jak widać, nie każdy musi wszystko lubić

elpe:

	1
C(9,4) prosta AC=12x−12 środek AC=(4		,2) dobrze czy juz to coś padło xD
	2

Basiek : Wszystko mi się zgadza, za wyjątkiem środka

	1+9		4+0
M(		,		)=M(5,2)
	2		2

elpe: źle |AC|=(5;2) i rownanie przechodzace przez środek prostej AC ma postac y=−2x+12 xD

Basiek : Twoje oznaczenia są kosmiczne...

elpe: a pkt. M? nie wiem co i jak

elpe: ale zamieszałem jejuu....

Basiek : M to jest ten środek przecież Tak sobie go nazwałam.

elpe: no przepisałem i juz wiem co i jak dzięki Basiek za chwile pewnie zgloszę sie po kolejna podpowiedź

pigor: ... lub od razu, bo masz punkt i wektor kierunkowy prostej jej równanie kanoniczne :

x−1		y
	=		, które jest ⇔ (x,y)=(8t+1, 4t)− postaci parametrycznej , a
8		4

dalej ⇔ 4x−4=8y ⇔ x−2y−1 = 0 − postać ogólna i wreszcie stanowczo za często używana w szkołach − aż do matury (a o innych prawie nic) − postać y=¹₂x−¹₂ − kierunkowa , o której ja ... wspominam i stosuję w ... ostateczności

Basiek : Wiesz co? Ja wychodzę. Może ktoś inny CI podpowie w tym czasie, lub poczekaj na mnie, ja będę punkt 20:00.

elpe: jak BD to pisz bo juz mam pytanie

Basiek : No, uciekł mi autobus−> nigdzie się nie wybieram−> jestem.

elpe: hahah bardzo dobrze masz może testy operona 2011 R , bo by mi to ułatwiło pytanie

Basiek : Niestety Operon omijam szerokim łukiem. 1,2,3 klasa zbiory Pazdro, Aksjomat rozszerzenie i podkowa rozszerzenie. To cały mój dorobek

elpe: a na Kiełbasie nic nie działasz? no to mam takie pytanie do zadania "Określ za pomocą układu nierówności trójkąt o wierzchołkach A=(−7,4),B=(−3,−2),C=(−3,4)." zadanie stosunkowo proste ale coś mi nie wychodzi prosta BC A co do Pazdro mnie dziś jeszcze czeka jeden arkusz.

Basiek : Kiełbasę w sumie jak coś chcę, to też drukuję, ostatnio bawiłam się z prawdopodobieństwem z tego zbiorku Jej, myślę... 4=−3a+b => −3a=4−b −2=−3a+b=> −2=4−b+b => sprzeczność... co bym nie zrobiła z tym− sprzeczność mi wychodzi.

elpe: a wychodzi z odp że od |BC|−−−−> x=−3 no ale nic jedziemy dalej

Basiek : Prosta prostopadła do OX: a=tg90st, a taki tg nie istnieje jedynie postać ogólna: Ax+By+C=0 {−3A−2B+C=0 {−3A−4B+C=0 Tu mi z kolei mam za dużo niewiadomych...

elpe: Dana jest prosta l o równaniu y=¹₂x+2 Znajdź pkt A należacy do prostej l, równo odległy od punktów P=(1,0), R+(5,2) co mi polecasz na zblizajace sie ferie, bo chciałbym podtrenować tą analityczna?

Basiek : Przez to wcześniejsze zadanie nie będę mogła spać... Ech. pkt A (x,y) przy czym ma leżeć na prostej l: więc y=U{1]{2}x+2 A(x,U{1]{2}x+2) wzór na odległość dwóch punktów zastosuj dwukrotnie dla AP i AR− porównaj, bo mają być równe. (odległość dwóch punktów= długość prostej)

Basiek : Elpe w tym poprzednim.... prosta x=−3 ....

elpe: DONE! a teraz takie cudeńko Punkt a+(2,1) jest wierzchołkiem trojkąta równobocznego ABC Bok Ab tego tórójkąta jest równoległy do osi OX wyznacz współrzedne wierzchołkow B i C tego trójkata wiedzac ze jego bok ma dł. 6 a cały trojkat jest zawarty w 1 cwiartce układu

elpe: jak to obliczyłaś ?

Basiek : O, fajne. To tak Jeśli A=(2,1), a bok AB jest równoległy to OX, to wiesz, że B(b,1) −> wynika wręcz z rysunku No i potem długość IABI=6 oblicz potem znajdziemy C

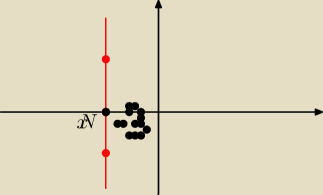
Basiek : No... tak to się mniej wiecej ma... a gdyby to była taka pozioma prosta, to y=−3 np. bo wszystkie pkt o takiej współrzędnej leżą na tej prostej

elpe: no mamy pkt A i B i co teraz?

Basiek : masz dwie drogi (a nawet 3 jakby liczyć tu wektory), więc: C(c,d) 1) IACI=6 i IBCI=6 układ równań− dwie niewiadome− rozwiązujesz− jest. 2) Skoro to równoboczny, to C leży na prostej prostopadłej do prostej AC i przechodzącej przez środek odcinka AB => wyliczasz współrzędne M. Wysokość trójkąta (CM) jest wysokością trójkąta

	a√3
równobocznego, więc ma dł.		= 3√3
	2

IMBI=3√3

elpe: licząc IACI=6 i IBCI=6 dochodzę do tego ze C(5; d) i nie wyliczę tego 'd' działajac z tym że IACI=6 czy już powinienem iść odpocząć

Basiek : Ojej, gapa ze mnie. Tak to jest jak się robi opisy, a zadanie nie rozwiązuje. Cóż, prawda to.

elpe: a nic się nie stało chociaż mi ulżyło

Basiek : Ej! A(2,1) B(8,1) IACI=6 IBCI=6 Masz dwie niewiadome dla C(c,d) i podwójny układ równań. MUSI się dać.

Basiek : Hahaha, kobieta zmienną jest jednak. Da się. Licz, licz

elpe: no to sprawdź bo ja juz sie poddaje

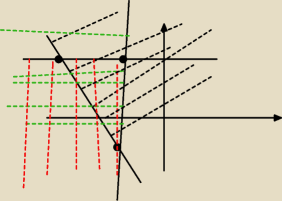
krystek: I pomyślcie jaki jest układ nierówności aby był Δ

elpe: "co ja pacze" haha

elpe: cały trojkat ma byc zawarty w 1 cwiartce

Basiek : hm wszystko pod pierwiastkiem: (2−c)²+(1−d)²= (8−c)²+(1−d)² 4−4c+c²+1−2d+d²= 64−16c+c²+1−2d+d² 12c=66 c=5,5 d=... to sobie spokojnie z czegokolwiek doliczysz, tak?

krystek: Z 18:23 zadanie !

Basiek : Ale ja umiem ;> Tylko prostej wyliczyć nie mogłam. Miałam przyjemność robić takiego typu zadanie na tablicy i śmiem twierdzić, ze nigdy nie zapomnę, jak coś takiego zrobić.

krystek: @ Basiek , nie wątpię !

elpe: uuu prowokacja

Basiek : To jest raczej przykre wspomnienie, jeśli o to chodzi. Ale dzięki temu na pewno zapamiętam.

elpe: no mam wszystko wielkie dzieki Basiek

Basiek : To dobrze.