| x2 | ||
√2 − x2 − | ||
| √2 − x2 |
 czyli łopatologicznie (bo boję się, że sie zamęczysz ) to tak :
czyli łopatologicznie (bo boję się, że sie zamęczysz ) to tak :
| 1 | ||
(x√2−x2)' = (x)' *√2−x2 +x *(√2−x2)' = 1√2−x2+ x * | * (2−x2)' = | |
| 2√2−x2 |
| x *(−2x) | (√2−x2)2−x2 | 2−x2−x2 | ||||
= √2−x2+ | = | = | = | |||
| 2√2−x2 | √2−x2 | √2−x2 |
| 2−2x2 | 2(1−x2) | |||
= | = | . ...  | ||
| √2−x2 | √2−x2 |
 ⇔ licznik się zeruje , czyli ⇔ 1−x2=0 ⇔ |x|=1 ⇔ x= ±1
⇔ licznik się zeruje , czyli ⇔ 1−x2=0 ⇔ |x|=1 ⇔ x= ±1 
| 4x − 4x3 | −4x(x − 1)(x + 1) | |||
y' = | = | = | ||
| 2√2x2 − x4 | 2x√2 − x2 |
| −2(x − 1)(x + 1) | ||
= | ||
| √2 − x2 |
 w tych x są asymptoty pionowe , czyli x=±√2 − równania asymptot pionowych
,
a nie miejsca zerowe funkcji
w tych x są asymptoty pionowe , czyli x=±√2 − równania asymptot pionowych
,
a nie miejsca zerowe funkcji 

 Założenie dla funkcji: −x2 + 2 ≥ 0, −(x + √2)(x − √2) ≥ 0
Dziedzina funkcji: x∊<−√2, √2>
Dziedzina pochodnej funkcji: x∊(−√2, √2)
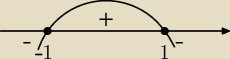
y' = 0 dla x = −1 oraz dla x = 1
Pochodna zmienia znak z minus na plus w punkcie x = −1, jest tu minimum.
Pochodna zmienia znak z plus na minus w punkcie x = 1, jest tu maksimum.
Założenie dla funkcji: −x2 + 2 ≥ 0, −(x + √2)(x − √2) ≥ 0
Dziedzina funkcji: x∊<−√2, √2>
Dziedzina pochodnej funkcji: x∊(−√2, √2)
y' = 0 dla x = −1 oraz dla x = 1
Pochodna zmienia znak z minus na plus w punkcie x = −1, jest tu minimum.
Pochodna zmienia znak z plus na minus w punkcie x = 1, jest tu maksimum.