Znajdź współrzędne środka okręgu opisanego na trójkącie o wierzchołkach:
Sławek: Witam!
Mam takie zadanko.
Znajdź współrzędne środka okręgu opisanego na trójkącie o wierzchołkach:
A=(6,1) B = (−2,5) C= (−6,−1)
Narysowałem sobie ten trójkąt i obliczyłem jego długości. Wyszło mi, że to jest trójkąt
równoramienny..
Dlaczego nie można tego policzyc w taki sposób, że wyznaczam prostą przechodzącą przez A i C a
nastepnie wyznaczam równanie kierunkowej prostej prostopadłej do niej i przechodzącej przez
pkt. B i licze pkt przecięcia się tych prostych? Wg. mojego rysunku to wlasnie ten punkt
powinien być środkiem okręgu.
2 lut 15:02
Aga1: Środek okręgu, to punkt przecięcia się symetralnych boków.
A może jest to trójkąt prostokątny równoramienny?
2 lut 15:05
Sławek: niewiem nic o kątach
2 lut 15:06
ICSP: ja bym układ równań zrobił i z głowy.
Każdy punkt należy do tego okręgu. Mamy trzy równania i trzy niewiadome.
2 lut 15:07
ICSP: ja bym układ równań zrobił i z głowy.
Każdy punkt należy do tego okręgu. Mamy trzy równania i trzy niewiadome.
2 lut 15:08
Sławek: ale ja nie umiem niestety rozwiazywac równan z 3 niewiadomymi
2 lut 15:09
Sławek: i o ile wiem, do matury podstawowej chyba nie potrzebuję tej umiejetnosci.
czy sie myle? ;>
2 lut 15:09
Sławek: aaa i jeszcze takie pytanko..
Ta zasada, że środek przecięcia się symetralnych trójkąta to środek okręgu tyczy się jakich
trójkątów?
2 lut 15:11
Sławek: Bo kurde te trójkąt jest równoramienny a nie równoboczny. Wiec ma tylko jedną oś symetri. Wiec
jak mozna liczyc srodek z jego symetralnych, nie kumam
2 lut 15:11
Aga1: Napisz równania symetralnych boków np AB i AC. punkt przecięcia symetralnych znajdziesz
rozwiązując układ z tych symetralnych.
Chyba szybciej jak Ci proponował ICSP
2 lut 15:14
Sławek: napewno szybciej ale nie umiem rozwiazywac układów równan 3 stopnia
2 lut 15:15
Sławek: Powiedzcie mi tylko, w przypadku których trójkątów działa ta zasada, że jego symetralne
przecinają się w środku okręgu na nim opisanego?
2 lut 15:16
Sławek: ii jak trójkąt równoramienny moze miec 3 symetralne ?!
Do tej pory byłem pewien, że trójkąt równoramienny ma 1 oś symetri. Tyle lat mi taki kit
wciskano?
2 lut 15:17
krystek: Przeciez będziesz miał układ dwóch równań, czytaj uważnie co napiała Aga1
2 lut 15:17
Kejt: oś symetrii i symetralna to nie to samo...
2 lut 15:17
Aga1: To co napisałam o symetralnych boków dotyczy każdego trójkąta.
W trójkącie prostokątnym środek okręgu opisanego na nim znajduje się na środku
przeciwprostokątnej, a w równobocznym pokrywa się ze środkiem przecięcia się środkowych.
Wzór podawałam, poszukaj.
2 lut 15:19
Sławek: tak ale Aga odnosiła się do sposobu ICSP, czyli tego w którym pod równanie okręgu będe musiał
podstawić 3 punkty. A to będzie układ równań z 3 niewiadomymi.
2 lut 15:19
2 lut 15:20
Sławek: czyli jezeli bym w prostokątnym poprowadził jego symetralne to tez wyznaczylyby mi srodek
okręgu? Tak wiem , ze w prostokątnym srodek jest 1/2 przeciwprostokątnej ale chce sie upewnic
2 lut 15:21
Sławek: ok krystek, rozumiem
Czyli symetralna to nie to samo co os symetrii
2 lut 15:22
Aga1: Symetralna odcinka na ogół ≠oś symetrii ( tylko w trójkącie równobocznym te proste pokrywają
się.)
2 lut 15:23
Sławek: rozumiem
2 lut 15:23
Sławek: A jakbym od prostokątnego wyznaczyl 3 symetralne jego boków to tez przeciely by sie w srodku
okreguu na nim opisanego?
2 lut 15:24
Aga1: Jak najbardziej.
2 lut 15:25
krystek:
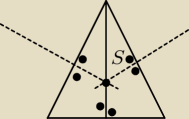
2 lut 15:25
Mila: Sławek, mylisz pojęcia, to co chciałeś napisać to równanie wysokości. Napisałeś równanie AC,
znajdź środek s1 odcinka AC i napisz równanie prostopadłej przechodzącej przez s1.
Tak samo z prostą AB ijej symetralną.
2 lut 15:25
Sławek: zaczynam juz wszystko łapać.
2 lut 15:26
Sławek: Dziękuje za pomoc.
Mam nadzieję, że kiedys osiągne taki poziom, ze tez bede w stanie Wam pomóc
Pozdrawiam!
2 lut 15:27
Aga1: Trzymamy Cię za słowo.
2 lut 15:28
krystek: Oj ,Dziecko to mnie na świecie nie będzie już !W której klasie jesteś?
2 lut 15:30
paulina:
24 sty 16:58
