geometria analityczna

geometria analityczna jarke: Jaki kąt tworzy z osią OX dana prosta?

	√3
b)		x + y =1
	3

c) x + y = 3 mam problem, gdy współczynnik a jest ujemny, czyli znajduje się w drugiej ćwiartce, coś ze wzorami redukcyjnymi chyba trzeba zrobić, ale błądzę i błądzę... przykład d): 9x−3√3y=4 zrobiłem bez problemu a z powyższymi nie daje rady. proszę o wytłumaczenie, nie o gotowca.

2 lut 01:05

ICSP:

	√3
b) y = −		x + 1
	3

	√3
tgα = −
	3

patrzysz na wykres i odczytujesz wartość α α = 150^o

2 lut 01:08

ICSP: c) 135^o

2 lut 01:08

jarke: trochę średnio odczytać z wykresu, który jest w tablicach... ;f

2 lut 01:16

ICSP: hmmm. Możesz zawsze zrobić "urojony" w głowie.

2 lut 01:17

ICSP: ale skoro jesteś fanem wzorów redukcyjnych : tg(90^o + α) = −ctgα rozważmy twój przykład :

	√3
tgα = −		= −ctg60^o
	3

Widzisz zależność?

2 lut 01:19

jarke: naucz mnie tworzyć taki dokładny

2 lut 01:19

Basiek : hm. tg ujemny dla 2ćw i 4ćw. tg150=tg(180−30)= tg(−30)=−tg30 (od tyłu) dlaczego nie uwzględniamy 4−tej ćwiartki?

2 lut 01:21

jarke: wiem już jak!, rozumiem! P[Basiek] dobre pytanie

2 lut 01:23

jarke: aaa, Basiek, dobre pytanie! tak miało być nooo

2 lut 01:24

Basiek : Wszystkie moje pytanie są dobre, za wyjątkiem tych, które są głupie.

2 lut 01:24

ICSP: ponieważ kąt nachylenie prostej musi się zawierać w przedziale <0;π)

2 lut 01:25

jarke: hehe

no tak, logiczne

2 lut 01:26

Basiek : Ale wiesz co? Tak mi się wydaje, że to po prostu kąt dopełniający dla tego z drugiej ćwiartki... np. patrz do drugiego: http://www.wolframalpha.com/input/?i=x+%2B+y+%3D+3+ 135 st. będzie dla ćw. 2−giej, zaś dla 4−tej kąt dopełniający... 45.

2 lut 01:27

Basiek : Chociaż nie, nie wiem. Nieważne. Nigdy nie widziałam rysunku, gdzie nachylenie kąta jest zaznaczone pod osią OX.

2 lut 01:29

jarke: no tak, zgadzam się... w odpowiedziach wyniki się zgadzają 150^o i 135^o... więc chyba tak być musi że I i II ćwiartka

2 lut 01:31

Basiek : Ja popieram tę teorię

2 lut 01:31

jarke: w drugą stronę to chyba ujemne kąty, przeciwko ruchowi wskazówek zegara zawsze dodatnie kąty! jakoś tak to było

2 lut 01:32

ICSP: hmmm skoro tak wam sie zachciało innych ćwiartek do dlaczego nie rozpatrujemy kątów z przedziału : <100000π;100001π)

2 lut 01:34

Basiek : Wciąż wredny emotka

2 lut 01:35

jarke: bo łatwiej można się pomylić i z reguły chyba zaczyna się na początku układu współrzędnych

2 lut 01:35

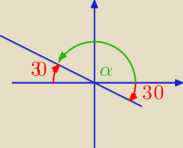
Godzio: rysunek

Albo tak się nauczyć:

	√3		√3
tgx = −		każdy wie, że jeżeli x = 30^o to tgx =		, jeśli dodamy minusa:
	3		3

	√3
x = −30^o to mamy tgx = −
	3

α = 180 − 30 = 150 emotka

2 lut 01:36

Basiek : http://www.megamatma.pl/res/upload/RYSUNKI_DOBRE/liceum/plik_6_2_2/3.gif Kąty skierowane: na zielono dodatni, na czerwono ujemny emotka

2 lut 01:37

ICSP: Basiek emotka

tuli tuli

2 lut 01:37

ICSP: Witaj Godzio przecież to jest odczytywanie z wykresu

2 lut 01:38

Godzio: Myślałem, że chodzi Ci o wykres tangensa

2 lut 01:39

Basiek : Sam jesteś odczytywanie z wykresu... Ciekawa droga.

"Like it"

2 lut 01:39

jarke: i ja myślałem, że chodzi o wykres tangensa...

2 lut 01:39

ICSP: tzn ja ma kilka wykresów na raz przed oczami

To jest jeden z nich

2 lut 01:40

jarke: tak czy inaczej, dzięki za pomoc : )

2 lut 01:50

krystek: A ja pozwolę sobie tutaj dodać swoje :

	√3
tgx=−
	2

tgx=−tg30 i teraz tg jest ujemny w drugiej ćwiartce( korzystamy ze wzorów redukcyjnych i mamy tgx=tg(180−30) x=150+k*180 i koniec . dla sin

	1
sinx=−
	2

sinx=−sin30 sinx=sin(180+30) lub sinx=sin(360−30) wzory red i znaki funkcji− f sin ujemna w III i IV ćw. x=210+k*360 lub x=330+k*360

2 lut 09:23