Wydaje mi się że można zastosować tutaj twierdzenie cos. ale nie wiem co dalej
Marek19: Wykazać że w dowolnym czworokącie suma kwadratów długości czterech boków jest
nie mniejsza niż suma kwadratów długości jego przekątnych
Artur z miasta Neptuna:
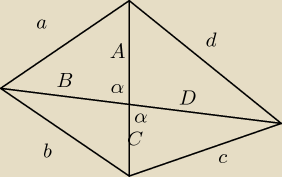
(*) Przyjmuję α≤90
o (dla większego 180 − α ≤90
o i dowód dla niego robi się analogicznie)
a
2 = A
2+B
2 − 2AB cosα
b
2 = B
2+C
2 − 2BC cos(180 − α)
c
2 = C
2+D
2 − 2CD cosα
d
2 = D
2+A
2 − 2DA cos(180 −α)
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
a
2+b
2+c
2+d
2 = 2*(A
2+B
2+C
2+D
2) + 2cosα( − AB − CD + BC + DA)
P = 2(A
2+B
2+C
2+D
2 + cosα[B(C−A) − D(C−A)]) = 2(A
2+B
2+C
2+D
2 + cosα[(B−D)(C−A)]) ≥
//(*)// ≥ 2(A
2+B
2+C
2+D
2 − 0 = (A+C)
2 + (B+D)
2 + (A−C)
2 + (B−D)
2 ≥ (A+C)
2+(B+D)
2