bryły obrotowe Lucy: Jaki jest promień kuli wpisanej w stożek którego wysokość jest równa √3 a promień podstawy wynosi 1

pigor: ... otóż , z warunków zadania R²+1² = (√3−R)² ⇔ R²+1² = (√3−R)² ⇔ R²+1 = 3−2√3r+ R² ⇔

	1
2√3R=2 ⇔ √3R =1 ⇔ R =		⇔ R = 13√3 − szukany promień
	√3

kuli . ...

Lucy: jest jakiś łatwiejszy sposób na zrozumienie tego zadania? albo bardziej przejżysty bo nie mogę się połapać..

pigor: ... niektórzy nazywają to gotowcem, ale do rzeczy narysuj sobie okrąg, opisz na nim trójkąt (przekrój osiowy stożka) i ... bardziej przejrzystego rozwiązania nie znajdziesz, tylko "odblokuj" swoją pamięć RAM (tę w głowie). pozostaję z nadzieją, że uda ci się to zrobić

Ewaa: potrzebuje zrozumieć to zadanie, a nie tylko spisać wynik co to jest R w tym zadaniu skoro promień wynosi 1?

pigor: widzę, że nadal masz blokadę, co to R przeczytaj do końca moje rozwiązanie, bo − po to cię uczyli czytać i i tam pisze co to jest

Ewaa: R²+1² = (√3−R)² ii to skąd się wzięło..? prooszę o odpowiedź

Ewaa: przepraszam ale czasami potrzeba czasu na zrozumienie czegoś naprawdę prostego, trochę wyrozumiałości.. nie każdy jest tak mądry

wmboczek: Można też tak − obliczamy długość tworzącej i wychodzi nam, że trójkąt jest równoboczny. R w takim trójkącie to 1/3 wysokości

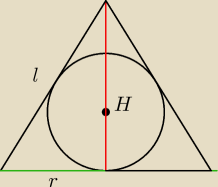
Aga1: r=1 H=√3 l²=r²+H² l=2 2r=2=l

	1
Trójkąt jest równoboczny, więc promień okręgu wpisanegow ten trójkąt jest równy		H
	3

	1		√3
Odp.R=		√3=		.
	3		3