Stereometria Tyrla: Oblicz pole powierzchni i objetosc ostroslupow (b,c) http://imageshack.us/photo/my-images/849/zdjcie0096o.jpg/

Artur z miasta Neptuna:

	1
V=		Pp*H
	3

1. wylicz P_p ze wzoru na P_prostokąta 2. wylicz P_p ze wzoru na P_{trójkąta prostokątnego} 3. wylicz P_p ze wzoru na P_rombu gdy dane są przekątne

Tyrla: a) obliczylem ale b i c nie chca wyjsc

Artur z miasta Neptuna: ale tutaj w niczym Ci nie pomogę ... musisz po prostu podstawiać DANE do wzorów o ile przy rombie jeszcze zrozumiem, że nie możesz wyliczyć boku rombu, o tyle w b. to zwykle dostawienie.

Tyrla: to mozesz mi pomoc w c)

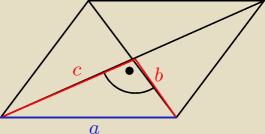
Artur z miasta Neptuna: podstawienie* a co do obliczenia boku rombu to masz (rysunek): b i c to połowy przekątnych ... a 'a' obliczasz z 'pitagorasa'

Tyrla: Pole podstawy w b) wychodzi 36√3 tak ?

Tyrla: Niech mi ktos pomoze

Tyrla: ?

rafal274: W przypadku b tam jest kąt prosty pomiędzy bokami a i b ?

Tyrla: tak

rafal274: To w takim razie skoro tam jest kąt prosty to pole podstawy to pole trójkąta prostokątnego, czyli :

	1		1
P =		*a*b =		*12*5 = 30
	2		2

Tyrla: A pole boczne ?

rafal274: I dalej tam wysokośc chyba też jest prostopadle na bok a oraz na bok b, tak ? jeżeli tak to masz kolejne 2 trójkąty gdzie wystarczy policzyc pole. Następnie pozostaje trzeci trójkąt. Wyznaczamy jego trzy boki z tw. Pitagorasa oraz liczymy pole ze wzoru Herona, czyli :

	1
p =		(d + e + f) = połowa obwodu trójkąta. boki d, e, f to są te trzy przeciwprostokątne
	2

tamtego trójkąta, który nie jest połączony z bokami, a, b, h Następnie wzór na pole takie trójkąta to : S = √p(p−d)(p−e)(p−f)

rafal274: Jak obliczysz pola wszystkich 4 trójkątów to masz pole powierzchni tego ostrosłupa.

Tyrla: a podpunkt c) ?

rafal274: W przypadku c w podstawie mamy romb. Liczymy Pole tego rombu stosując wzór na przekątne rombu, czyli :

	1
P =		* d1*d2 =
	2

Następnie wiemy, że przekątne w rombie dzielą się na połowy. Wysokość jest pod kątem prostym opuszczona na te połowy. możemy stosując twierdzenie Pitagorasa obliczyć krawędzie ścian bocznych tego ostrosłupa.

rafal274: Następnie połówki przekątnych rombu przecinają się pod kątem prostym jak na rysunku, czyli po raz kolejny z tw. Pitagorasa liczymy bok rombu. I jak widzisz Ściany boczne są trójkątami, gdzie będziemy znać boki (krawędzie) oraz bok podstawy (rombu). I znowu stosujemy bardzo przydatny wzór Herona

rafal274: A Objętość ostrosłupa to już chyba formalność.

Tyrla: Nie chce mi wyjsc pole boczne w b)

rafal274: Policzę

Tyrla: Dzieki

Tyrla: I jakbys mogl tez od razu c) policzyc

rafal274: P_b = ¹₂ * (ab + bh + ah) + Z = ¹₂ * (12*5 + 5*11¹₁₃ + 12*11¹₁₃) + Z = = 248⁴₁₃ + Z; Teraz wyznaczam trzy boki trójkąta Z, czyli, : d = √a² + b² = √5² + 12² = 13 cm

	√24961
e = √a2 + h2 = √52 + (11113)2 =
	13

	√45072
f = √b2 + h2 = √122 + (11113)2 =
	13

g = połowa obwodu trójkąta

	√45072 + √24961 + 169
g = 12 * d * e * f =
	26

	√45072 + √24961 − 169
g − d =
	26

	√45072 − √24961 + 169
g − e =
	26

	−√45072 + √24961 + 169
g − f =
	26

Z = √g(g−d)(g−e)(g−f) = 78 Wracamy : P_b = 248⁴₁₃ + Z = 248⁴₁₃ + 78 = 226⁴₁₃

rafal274: Sorry, że tak długo, ale z psem trzeba też wychodzić

Tyrla:

	2
Cos chyba jest nie tak bo pole calkowite wyszlo 202
	13

Tyrla: ?