ekstrema
Dawid: eksterma
f(x) = (x+2)ex
f'(x)= (x+2)'*ex + (x+2)ex = ex + ex(x+2) = ex (1+(x+2)) = ex(x+3) −− =0 dla x= −3
funkcja nie zminia znaku czyli nie ma ekstrmy ?
1 lut 13:06
ZKS:
Jak to nie zmienia znaku?
ex jest dla każdego x większa od 0 więc o znaku pochodnej decyduje x + 3 = 0 a to zmienia znak
z minusa na plus.
1 lut 13:13
Artur z miasta Neptuna:
a niby dlaczego x= 0 ?
Ile to e
0 
0

niee ... 1
jak pochodna nie zmienia znaku w punkcie 'zerowym' wtedy funkcja f(x) nie ma ekstremum.
Aby pochodna 'nie zmieniała znaku' w punkcie x
0, punkt x
0 musi być 2n−krotnym pierwiastkiem
(czyli np. dla f(x) = x
3, f' = 2x
2 x
0=0 jest 2−krotnym pierwiastkiem, więc w x
0=0
funkcja f(x) nie posiada ekstremum <tylko punkt przegięcia>)
1 lut 13:13
ZKS:
Źle Artur z miasta Neptuna interpretujesz zapis.
Tam jest napisane ex(x + 3) = 0 dla x = −3 więc jest rozwiązane poprawnie.
1 lut 13:15
Dawid: czyli w koncu jak?
1 lut 13:17
Dawid: czy jest to przypdakiem minimum lokalne nie własciwe ?
1 lut 13:18
Aga1:
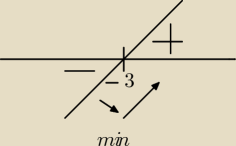
1 lut 13:20
Dawid: acha juz rozumem z ta zmiana znaku dzieki
1 lut 13:21
ZKS:
A jak pochodna zmienia znak z minusa na plus to jakie jest to ekstremum?
1 lut 13:22
Aga1: ymin=f(−3)=−e−3.
1 lut 13:22
Dawid: minimum

1 lut 13:24
ZKS:
Jak
Aga Ci napisała to już nie problem było napisać jakie to ekstremum.

1 lut 13:26
Dawid: nie zrozumialem na pocztaku zmiany znaku dlatego nie wiedzialem a tak to wiem kiedy jest min a
| | sin(x−2) | |
kiedy max  to jeszcze takie zadanko lim x−2 |
| rozwiazywalem ale |
| | 3x−2−1 | |
nie radze sobie z mianownikiem

1 lut 13:30
Dawid: zmierza to do 00 i z D.Hospitala tak?
1 lut 13:31
Artur z miasta Neptuna:
tak ... z d'Hospitala
1 lut 13:33
ZKS:
| | | | 1 | |
= |
| = |
| |
| | | | 3x − 2 − 1 | | limx → 2 |
| | | | x − 2 | |
| | ln3 | |
1 lut 13:35
Dawid: | | cos(x−2) | |
czyli limx→2 = |
| = 1 |
| | e(x−2)ln3 | |
1 lut 13:36
1 lut 13:36
Dawid: ok pisalem zanim sie pokazalo rozwiazanie
1 lut 13:37
ZKS:
I niestety Ci inna granica wyszła niż mi.
1 lut 13:39
Dawid: zle piliczylem pochodna z mianownika
1 lut 13:40
 0
0  niee ... 1
jak pochodna nie zmienia znaku w punkcie 'zerowym' wtedy funkcja f(x) nie ma ekstremum.
Aby pochodna 'nie zmieniała znaku' w punkcie x0, punkt x0 musi być 2n−krotnym pierwiastkiem
(czyli np. dla f(x) = x3, f' = 2x2 x0=0 jest 2−krotnym pierwiastkiem, więc w x0=0
funkcja f(x) nie posiada ekstremum <tylko punkt przegięcia>)
niee ... 1
jak pochodna nie zmienia znaku w punkcie 'zerowym' wtedy funkcja f(x) nie ma ekstremum.
Aby pochodna 'nie zmieniała znaku' w punkcie x0, punkt x0 musi być 2n−krotnym pierwiastkiem
(czyli np. dla f(x) = x3, f' = 2x2 x0=0 jest 2−krotnym pierwiastkiem, więc w x0=0
funkcja f(x) nie posiada ekstremum <tylko punkt przegięcia>)
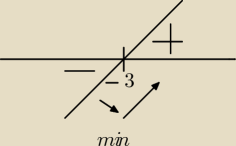


 to jeszcze takie zadanko lim x−2
to jeszcze takie zadanko lim x−2 