4 Róża: Oblicz cos kąta dwuściennego między ścianami ostrosłupa prawidłowego czworokątnego, w którym krawędzie podstawy równe są a, oraz kąt między krawędzią podstawy a krawędzią boczną równa się

	π
		.
	3

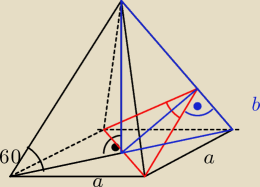
BigRedOne: Na początek sam rysunek.

BigRedOne: Liczę: a) Wysokość "H":

H		H		a√6
	= tg60o =>		= √3 = > H =
a√2   2		a√2   2		2

b) Krawędź boczną "d":

a√2   2		a√2   2		1
	= cos60o =>		=		=> d = a√2
d		d		2

BigRedOne: c) Teraz z podobieństwa w trójkątów (patrz duży niebieski i mały wewnątrz niego − cecha podobieństwa kkk):

a√6   2		x		a√6
	=		= > x =
a√2		a√2   2		4

d) Teraz, gdy mamy obliczoną wysokość czerwonego trójkąta potrzebny jest nam jego bok. Stosujemy tw. Pitagorasa:

	a√6		a√2
(		)2 +		= c2
	4		2

6a2		2a2
	+		= c2
16		4

6a2+8a2
	= c2
16

	14a2
c2 =
	16

	a√14
c =
	4

e) Ostatni krok. Stosujemy tw. Cosinusów do wyliczenia cosinusa kata w czerwonym trójkącie:

	14a2		a√14
(a√2)2 = 2*		−2*		*cosα
	16		4

I tutaj oblicz... Pisze to bardzo późno, dlatego mogłem się pomylić w obliczeniach ale poprawisz sobie i będzie dobrze

BigRedOne: O BOŻE TO KAT POMIĘDZY KRAWĘDZIĄ BOCZNĄ A KRAWĘDZIĄ PODSTAWY A NIE PŁASZCZYZNĄ PODSTAWY... W TAKIM RAZIE MOJĄ ROBOTĘ CH...J TRAFIŁ EHH...

P@weł: Heheheh 35 minut życia zmarnowales