dvdvd jarkoski:

	1		2
siemka mamy takie cos: rozwiaz rownanie:		=
	|3−x|		|2x−1|

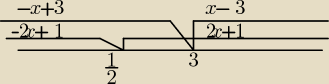
ja robie takie rzeczy tak jak na rysunku i nie proszę o rozwiazanie bo takowe mi wyszlo ale prosze wytlumaczcie mi dlaczego to mi wychodzi tylko wtedy gdy |3−x| zapisuje jako |x−3| tzn wiem skąd to sie bierze ale dlaczego ten zabieg jest konieczny ? nie moze zostac 3−x pozdro

Mila: Też wyjdzie, tylko trzeba wiedzieć jaki znak ma wyrażenie w odpowiednim przedziale. Łatwiej jest, gdy najpierw (od lewej na osi, wyrażenia są ujemne. Pytaj , jeśli dalej nie rozumiesz. Wartości bezwględne są ważne.

jarkoski: tzn nie wiem jak to widzisz

Aga1: Jedna z wielu własności. Ix−yI=Iy−xI dla x,y∊R Odległość z Warszawy do Gdańska jest taka sama jak z Gdańska do Warszawy.

jarkoski: no ja wiem skad ta wlasnosc wynika ale jak zrobic nei zmeniając tego

Ja: tu chyba jakieś nierówności powinny być

Aga1: I3−xI=3−x, gdy 3−x≥0, x≤3 I3−xI=x−3, gdy 3−x<0,x>3

jarkoski: aaa ! a czy to nie jest tak ze jak mam ymodul |3−x| to on jest ujemny w przedziale (−∞;3) ? a dodatni <3;∞) i przyjmujes postac −3+x ?

Mila: Zapisuję: x−3≥0⇔x≥3 2x−1≥0⇔x≥0,5 mam na osi przedziały: (−∞,0,5)∪<0,5;3)∪<3,∞) w pierwszym przedziale obydwa wyrażenia są ujemne , zmienia je na przeciwne , dalej tłumaczyc, czy napiszesz równanie?

jarkoski: dokladnie Dziekuje Aga

pigor: ... a dla mnie "kochani" ... czas to pieniądz i dlatego ja bym ... widział to tak : I sposób :

1		2
	=		⇔ 2 |−(3+x)| = 1 |2x−1 ⇔ 2 |−1||x−3| = 2 |x−12| ⇔
|3−x|		|2x−1|

|x−3|=|x−¹₂| ⇔ czyli równoodległa od 3 i ¹₂ jest liczba x=³₂=1,5 , a II sposób :

1		2
	=		⇔ 2|3−x|="2x−1| /2 obustronnie ⇔ 4(3−x)2=(2x−1)2 ⇔
|3−x|		|2x−1|

4(9−6x+x²)=4x²−4x+1 ⇔ 36−24x = −4x+1 ⇔ 20x=35 ⇔ x= ⁶₄=³₂=1,5 . ...

Aga1: Mała poprawka 20x=35//:20

	7
x=
	4

pigor: o kurcze . ... faktycznie dzięki Aga − przepraszam, nie umiem dzielić

	3−0,5		2,5		3		7
		=		=1,75=1		=		. ...
	2		2		4		4

Aga1: Jeszcze inny sposób. Rozwiązanie należałoby rozpocząć od wyznaczenia dziedziny.I3−xI≠0 i I2x−1I≠0

	1
D=R−{		, 3}
	2

Skorzystać z proporcji i ze wzorów IaI*IbI=Ia*bI, IaI=IbI⇔a=b lub a=−b 2I3−xI=I2x−1I I6−2xI=I2x−1I 6−2x=2x−1 lub 6−2x=−2x+1 4x=7 0=−5 równanie sprzeczne

	7
Odp x=		.
	4