Oblicz długośc boku kwadratu wpisanego w trójkąt
NieopodalLasku:
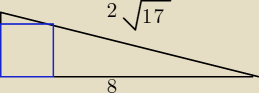
Oblicz długosc boku kwadratu wpisanego w trójkąt prostokątny o przyprostokątnej równej 8 i
przeciwprostokątnej równej 2
√17
31 sty 17:32
NiepodalLasku: Jest ktoś w stanie wykonać to zadanie?
31 sty 20:06
al:
oblicz drugą przyprostokątną ( 2), x−dł. boku kwadratu
31 sty 20:20
Eta:
x −−− dł. boku tego kwadratu
x= 1,6
31 sty 20:20
DuzeOko: A skąd wziąłeś to 2? jest jakis wzór?
31 sty 20:24
Eta:
Pitagoras

b
2=c
2−a
2 b
2= (2
√17)
2−8
2
b=.........
31 sty 20:25
DuzeOko: Dobrze, z pitagorasa wychodzi, że 2 przyprostokątna to 2 ale proszę, wytłumacz mi jak dokładnie
teraz obliczyc ten jeden bok bo z tego co napisal al nie moge niz wywnioskować
31 sty 20:30
al:
to podobieństwo trójkątów
31 sty 20:31
DuzeOko: tzn, mozesz podac do tego jakiś link?
31 sty 20:40
al:
jeżeli trójkąty mają takie same kąty, to są podobne, a zatem boki mają proporcjonalne
możesz ułożyć też proporcję z tw. Talesa
31 sty 20:43
Eta:
 al
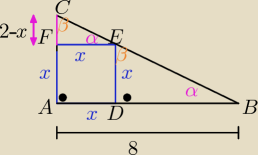
al wykorzystał podobieństwo
| | 2 | | 2−x | |
ΔABC ~ ΔFEC ⇒ |
| = |
| |
| | 8 | | x | |
31 sty 20:48
DuzeOko: Czemu 2−x?
31 sty 21:26
al:
bo FC=AC−AF=2−x
31 sty 21:28
DuzeOko: A już kapuje, dziękówka
31 sty 21:32
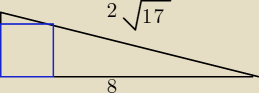 Oblicz długosc boku kwadratu wpisanego w trójkąt prostokątny o przyprostokątnej równej 8 i
przeciwprostokątnej równej 2√17
Oblicz długosc boku kwadratu wpisanego w trójkąt prostokątny o przyprostokątnej równej 8 i
przeciwprostokątnej równej 2√17
 b2=c2−a2 b2= (2√17)2−82
b=.........
b2=c2−a2 b2= (2√17)2−82
b=.........
 al wykorzystał podobieństwo
al wykorzystał podobieństwo