 otóż, niech dwusieczna kąta DAB dzieli ten kąt na dwa równe kąty α i
przecina
dwusieczną kąta CDA w punkcie O, która z kolei przecina bok AB w punkcie E i dzieli ten
kąt CDA na 2 równe kąty β (zaznacz te kąty α i β na swoim rysunku , to
∡AED|= |∡CDE| = β , zatem Δ AED − równoramienny o kątach β przy postawie, a to
oznacza, że AO jest wysokością względem podstawy tego trójkąta , czyli
AO ⊥ DE − z własności wysokości trójkąta , a to należało uzasadnić . ...
otóż, niech dwusieczna kąta DAB dzieli ten kąt na dwa równe kąty α i
przecina
dwusieczną kąta CDA w punkcie O, która z kolei przecina bok AB w punkcie E i dzieli ten
kąt CDA na 2 równe kąty β (zaznacz te kąty α i β na swoim rysunku , to
∡AED|= |∡CDE| = β , zatem Δ AED − równoramienny o kątach β przy postawie, a to
oznacza, że AO jest wysokością względem podstawy tego trójkąta , czyli
AO ⊥ DE − z własności wysokości trójkąta , a to należało uzasadnić . ...
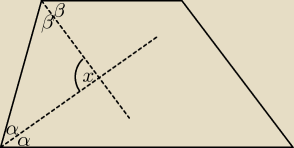 2α + 2β = 180o
α + β = 90o
x = 180o − (α + β) = 180o − 900 = 90o
2α + 2β = 180o
α + β = 90o
x = 180o − (α + β) = 180o − 900 = 90o