 parabola z ramionami skierowanymi do dolu, przechodzi przez te dwa pkt, z czego P=(−1,3) jest
wierzcholkiem paraboli, nie ma okreslonych miejsc zerowych.
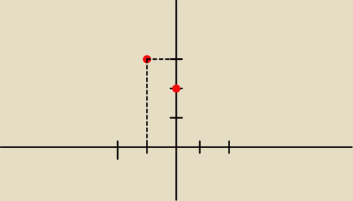
Na rysunku obok przedstawiony jest fragment paraboli, ktora jest wykresem funkcji kwadratowej
f.
a) napisz wzor funkcji w postacji kanonicznej
b)oblicz miejsca zerowe
c)naszkicuj wykres g(x)=f(x−4)
zrobilam pkt a) i odpowiedz mam y=−(x+1)2 +3
b) miejsca zerowe
y= 0 dla jakich x?
0=−(x+1)2+3
0=−x2−2x+2
delta=4−4*2*(−1)
delta=4+8
delta=12 √delta= 2√3
x1 = 2−2√3−2 i jak to dalej zrobic?
x2 = 2+2√3−2
parabola z ramionami skierowanymi do dolu, przechodzi przez te dwa pkt, z czego P=(−1,3) jest
wierzcholkiem paraboli, nie ma okreslonych miejsc zerowych.
Na rysunku obok przedstawiony jest fragment paraboli, ktora jest wykresem funkcji kwadratowej
f.
a) napisz wzor funkcji w postacji kanonicznej
b)oblicz miejsca zerowe
c)naszkicuj wykres g(x)=f(x−4)
zrobilam pkt a) i odpowiedz mam y=−(x+1)2 +3
b) miejsca zerowe
y= 0 dla jakich x?
0=−(x+1)2+3
0=−x2−2x+2
delta=4−4*2*(−1)
delta=4+8
delta=12 √delta= 2√3
x1 = 2−2√3−2 i jak to dalej zrobic?
x2 = 2+2√3−2
 teraz tak: f(x)= −(x+1)2+3
to wykres f(x−4) powstaje przez przesunięcie wykresu f(x) o 4 jednostki w prawo
teraz tak: f(x)= −(x+1)2+3
to wykres f(x−4) powstaje przez przesunięcie wykresu f(x) o 4 jednostki w prawo
| 2(1−√3) | ||
x1= | = −(1−√3)= −1+√3= √3−1 | |
| −2 |

 DZIEKUJE!
a jeszcze mam pytanko:
sprowadz do postaci kanonicznej:
f) y=−√2(x+3)(x−1)
y=−√2(x2+2x−3)
i znowu te pierwiastki, ktorych nienawidze
DZIEKUJE!
a jeszcze mam pytanko:
sprowadz do postaci kanonicznej:
f) y=−√2(x+3)(x−1)
y=−√2(x2+2x−3)
i znowu te pierwiastki, ktorych nienawidze 

| x1+x2 | ||
p= xw= | = ........ | |
| 2 |


