Mission Impossible
Kolejny taki nick.: Mission Impossible
Muszę koniecznie nauczyć się do przyszłej środy stereometrii na poziomie rozszerzonym. Chwilowo
moja wiedza nie przekracza podstawówki.
Dałoby się coś z tym zrobić? W sensie− czy pomożecie?


30 sty 21:50
ICSP: ależ oczywiście że pomożemy

My jesteśmy bardzo mili

30 sty 21:51
30 sty 21:56
ICSP: Dobra już sie nie wypowiadam w tym temacie

30 sty 21:57
Eta:
Wypijcie

na zgodę

30 sty 21:59
Też chcę inny nick!: Widzisz, umiem dochodzić do kompromisów


30 sty 21:59
Też chcę inny nick!: Zadanie 1 ( 8 pkt. )
W stożku tworząca o długości 16 jest nachylona do powierzchni podstawy pod kątem,
| | 4 | |
którego tangens jest równy |
| .Oblicz stosunek pola powierzchni bocznej do pola podstawy |
| | 3 | |
tego stożka.
Zadanie 2 ( 3 pkt. )
Prostokątny arkusz blachy o wymiarach 40 cm na 60 cm jest rozwinięciem powierzchni
bocznej walca. Oblicz objętość walca, którego wysokość jest równa krótszemu bokowi
prostokąta.
Zadanie 3 ( 7 pkt. )
Objętość prostopadłościanu, którego wysokość ma długość 10 cm, równa się 480 cm
3.
Stosunek długości krawędzi podstawy wynosi 3 : 4. Wyznacz miarę kąta nachylenia
przekątnej prostopadłościanu do płaszczyzny podstawy. Sporządź rysunek prostopadłościanu i
zaznacz szukany kąt.
Ku pamięci− na jutro.

30 sty 22:10
Aga1: To TY Basiek?
30 sty 22:15
Też chcę inny nick!: No tak

Witaj
Aga 
30 sty 22:18
Eta:


30 sty 22:18
Aga1: Na jutro te zadanka?
30 sty 22:20
Też chcę inny nick!: No tak sobie powtarzam... dziś mój mózg chyba już nie działa. A muszę się nauczyć do przyszłej
środy, więc... dam radę !

30 sty 22:21
Aga1: Na pewno .
30 sty 22:23
Też chcę inny nick!: Ktoś sobie wymyślił maturę rozszerzoną na lekcjach pisać...
Tylko problem w tym, że moja wiedza z gimnazjum nt stereometrii dotyczy tylko sześcianu.

Nie wiem, dlaczego ktoś zakłada, że "to było i mamy umieć"...
30 sty 22:24
Godzio: Mogę tylko powiedzieć powodzenia

Ja mam ferie 2 tygodnie

30 sty 22:36
Też chcę inny nick!: A jak jak będę mieć ferie, to niektórzy... no cóż.

A w ogóle, to moje ferie zaczynają się zaraz po tej maturze, w przyszły tyg, w środę, więc
przeżyję !
30 sty 22:38
Eta:
Hej
Godzio 
Jaką masz średnią ? ( maxa?

30 sty 22:40
elpe: róbcie róbcie tą stereometrie to i mi sie przyda

mam podobny dylemat

30 sty 22:44
Godzio:
Eta dzisiaj wyniki z analizy i algebry ... porażka

Ogólnie mam tak:
Psychologia: 4,5
Filozofia: 4
Logika: 3
Analiza: 4,5 (jutro bede oglądać prace z egz, − 18,5 / 24 −− brakuje mi 0,5 pkt do 5 bo z
ćwiczeń miałem 5 więc zobaczymy)
Algebra: 4,5 (tu mogę się pochwalić, napisałem egzamin najlepiej na kierunku, uff udało się

)
30 sty 23:05
Kasia: gratuluję takich wyników, oby tak dalej!

30 sty 23:07
Godzio: No i programowanie: 4

(dzięki
Trivialowi !

)
30 sty 23:08
Godzio: Dzięki

30 sty 23:09
Też chcę inny nick!: O, gratki
Godzio 
Jej, w koło sami mądrzy ludzie

30 sty 23:10
Eta:
No pięknie! Gratulacje i tak trzymaj

( echch ta logika !

30 sty 23:10
elpe: a na jakiej to uczelni, odbywa się to wszystko?

30 sty 23:11
Eta:
Takich będziemy mieć przyszłych
matematyków 
30 sty 23:13
Godzio:
Logika jest najgorsza, dzisiaj byłem (po egzaminie) na weryfikacji oceny

i odpytka była, ale
odpowiedziałem na wszystko więc jest ok

No ale trudno

30 sty 23:13
Godzio: PWr
30 sty 23:14
Eta:
Ja najbardziej lubiłam analizę

30 sty 23:16
Godzio:
Ja też


30 sty 23:20
Też chcę inny nick!: Okej. To ja utknęłam przy pierwszym, gdzie Z JAKIEGOŚ NIEWYJAŚNIONEGO powodu wychodzi mi źle.
Pomocy?

| Pb | | πrl | | l | | 16 | |
| = |
| = |
| = |
| |
| Pp | | πr2 | | r | | r | |
{H
2+r
2=16
2
| | H | | 4 | | 4 | |
{tgα= |
| = |
| => H= |
| r |
| | r | | 3 | | 3 | |
.... tu sobie dodaję/ mnożę etc.
r
2=92,16
r=9,6
| | Pb | | 16 | | 5 | |
Czyli powrót do wcześniejszego.... |
| = |
| = |
| |
| | Pp | | 9,6 | | 3 | |
Co NIE ZGADZA się z odpowiedziami...

31 sty 13:49
Aga1: Popraw tylko obliczenia 25r
2=16
2*9
31 sty 13:55
Też chcę inny nick!: No ale....
25r
2= 256*9
25r
2=2304 / :25
r
2=92,16
r=
√92,16=9,6
żeby już tak łopatologicznie... obawiam się, że nie rozumiem

31 sty 13:58
Aga1: Masz dobrze, ja wzięłam 16 zamiast 162
31 sty 14:04
31 sty 14:06
Też chcę inny nick!: Właśnie! Wydawałoby się, że jest ok, ale po wyliczeniu wszystkiego...
http://www.lo.olecko.pl/matematyka/pdf/stereometria.pdf
Tu są odpowiedzi. Widzisz, po przeliczeniu obu pól, stosunek wyjdzie inny. Tak jakbym ja
zamieniła H i r. Rozumiesz może, co tu się podziało?
31 sty 14:07
Też chcę inny nick!: Póki co, jestem najbliżej wyniku

31 sty 14:07
Godzio:
Nie wychodzi mi tak jak im

W każdym razie w dodawaniu się pomyliłem

31 sty 14:09
Godzio: | | 8 | |
Mi już |
| wyszło  |
| | 3 | |
31 sty 14:10
Też chcę inny nick!: Moja odp ≈1,7
Godzia odp≈ 2,7
Prawidłowa =1,25
;>
31 sty 14:11
Godzio:
16
2 = (4x)
2 + (3x)
2 = 25x
2
16 = 5x
| Pb | | πrl | | l | | 16 * 5 | | 5 | |
| = |
| = |
| = |
| = |
| |
| Pp | | πr2 | | r | | 48 | | 4 | |
Dla mnie pole boczne = πr
2 + πrl
31 sty 14:13
Też chcę inny nick!: Ok, już wiem !
| | 4 | |
Jest dobrze, po prostu przepisałam |
| i liczyłam stąd.... |
| | 3 | |
| | 3 | |
a w tamtym pdfie tg= |
| co fakt faktem zamienia H z r. I zagadka rozwiązana.  |
| | 4 | |
31 sty 14:14
Aga!.: JUŻ WIDZĘ
| | 3 | | 4 | |
tgα= |
| , a nie jak napisałaś |
| |
| | 4 | | 3 | |
31 sty 14:14
Też chcę inny nick!: 
No po prostu, to jest dla mnie całkiem naturalne...
I fakt faktem dla mnie pole boczne to chyba powinno być całe pole powierzchni bocznej..., ale
nie będę się sprzeczać. Wychodzi.

Dziękuję


!
31 sty 14:16
Aga1: Pole boczne = pole powierzchni bocznej, a nie pole powierzchni.
Pole powierzchni= pole powierzchni całkowitej.
31 sty 14:19
Też chcę inny nick!: Zad. 2 i Zad.3 − zrobione.
Chyba nie muszę przedstawiać?
To do zrobienia na potem− tj. ma za jakieś 2h?
Zadanie 4 ( 6 pkt. )
Asia chce rozlać 8 l soku malinowego do słoiczków w kształcie graniastosłupa prawidłowego
sześciokątnego, których wysokość jest równa dłuższej przekątnej podstawy. Wykonaj
odpowiednie obliczenia i odpowiedz, czy wystarczy jej 26 słoiczków, jeśli wysokość każdego z
nich jest równa 0,8 dm?
Zadanie 5 ( 5 pkt. )
Krawędź podstawy ostrosłupa prawidłowego czworokątnego ma długość 6 cm. Pole
powierzchni całkowitej tego ostrosłupa jest równe 108 cm2. Wyznacz miarę kąta nachylenia
ściany bocznej do płaszczyzny podstawy. Sporządź rysunek ostrosłupa i zaznacz szukany kąt.
Zadanie 6 ( 6 pkt. )
Dach pewnej budowli ma kształt ostrosłupa prawidłowego sześciokątnego. Krawędź boczna tego
ostrosłupa ma długość b, a miara kąta nachylenia tej krawędzi do płaszczyzny podstawy wynosi
α . Wyznacz objętość tego ostrosłupa i tangens kąta dwuściennego między ścianą boczną a
płaszczyzną podstawy.
Zadanie 7 ( 4 pkt. )
Agnieszka, planując wycieczkę za miasto, postanowiła kupić termos. W sklepie były dwa
rodzaje termosów: białe i czerwone. Biały termos miał średnicę dwa razy większą niż
czerwony, ale za to był dwa razy niższy.
a) Który z termosów ma większą pojemność? Odpowiedź uzasadnij.
b) Pojemność czerwonego termosu jest równa 0,75 litra. Jaka jest pojemność białego
termosu
31 sty 14:21
Basiek : Pytanie do zad. 6−tego.
Jak wygląda/ jaki to kąt "dwuścienny między ścianą boczną a płaszczyzną podstawy"?
Wystarczy, że ktoś mnie powiadomi, co wyznacza ten kąt

31 sty 17:47
Aga1: Kąt między wysokością ściany bocznej a wysokością trójkąta równobocznego ( bo sześciokąt
foremny można podzielić na trójkąty równoboczne.)
31 sty 17:56
Basiek : Dziękuję ogromnie <kwiaty>
Czyli wszystkie zad. z poziomu podstawowego skończone

31 sty 18:02
Basiek : W ogóle, jest jakiś przepis na to wyznaczanie właściwych kątów w stereometrii? Bo właśnie tego
nie umiem,a przynajmniej w największym stopniu.
31 sty 18:05
Aga1: Zaznaczenie prawidłowo kąta to podstawa.
31 sty 21:51
Basiek : Właśnie wiem, a ja ich za nic zaznaczyć nie mogę

Nie umiem,
31 sty 21:57
Aga1: Podaj konkretne zadanie.
31 sty 21:59
krystek:
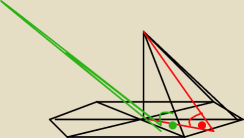
ten czerwony to kat między ściana boczna a pł podst.
31 sty 22:04
Basiek : Dla przykładu: (Ale prostszych też nie umiem ):
1) Płaszczyzna przekroju nachylona jest do płaszczyzny podstawy
2) Przekątna przekroju osiowego walca ma długość d i jest nachylona do płaszczyzny podstawy pod
kątem α .
3) sinus kąta nachylenia przekroju prostopadłościanu wyznaczonego przez te przekątne do
podstawy tego prostopadłościanu
No jak po chińsku dla mnie.
31 sty 22:05
Basiek : Czyli jeśli mam coś ze ścianą boczną, to najprawdopodobniej szukam jej wysokości i to jeszcze
na środku, tak? A potem od tego mam rysować jakąś prostą na podstawie i liczyć, że to będzie
to?

31 sty 22:06
krystek: a zielony to kąt nachylenia krawędzi bocznej do płaszczyzny podstawy (bazgroły zbędne)
31 sty 22:07
Basiek : Płaszczyznę ściany bocznej zawsze wyznacza jej wysokość?
31 sty 22:09
Aga1:
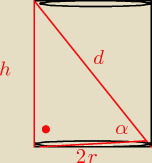
2)Przekrój osiowy walca jest prostokątem o wymiarach h na 2r.
Przekątna przekroju, to przekątna prostokąta
31 sty 22:10
krystek: mamy kąty dwuścienne ,między dwoma ścianami i mierzymy kątem liniowym ,tak jak napisałaś o
22;06(prostopadle do ich wspólnej krawędzi)
.
31 sty 22:12
krystek: w zad 1 napisz czego dotyczy ta pł przekroju to narysuje Tobie!
31 sty 22:16
Aga1: 1) i 3) wyrwane z kontekstu.
Jeśli w ostrosłupie masz powiedziane , że krawędź boczna jest nachylona do płaszczyzny podstawy
pod kątem α. to rysujesz trójkąt prostokątny zaczynając od spodka wysokości do wierzchołka,
potem schodzisz w dół po krawędzi i dochodzisz do spodka .
W utworzonym trójkącie ZAWSZE między wysokością ostrosłupa , a każdym odcinkiem w podstawie
jest kąt prosty.
31 sty 22:16
Basiek : Widzę światełko w tunelu!
Wcześniej nie wiedziałam, że jest jakaś różnica między dwuściennymi i liniowymi... w ogóle nie
wiedziałam, ze jest takie rozróżnienie!
Czy hm... jeśli jest to kąt dwuścienny to zawsze jest napisane "kąt dwuścienny między bla bla"
, czy jest jakiś haczyk, dzięki któremu powinnam te dwa rodzaje odróżniać?
31 sty 22:17
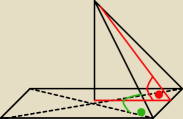
krystek:
31 sty 22:19
31 sty 22:21
Aga1: Kąt dwuścienny to jak sama nazwa wskazuje kąt miedzy dwiema ścianami bocznymi , między ścianą
boczną a podstawą( która też jest ścianą)
31 sty 22:22
krystek: Ponieważ nie wytłumaczono t
Tobie co to jest kąt dwuścienny −⇒to kąt utworzony przez dwie płaszczyzny o wspólnej krawędzi.
Mierzymy go kątem liniowym przecinajac prostopadlą płaszczyzna do ich wspólnej krawędzi .
Weź kartke zegnij ja pod pewnym kątem . Następnie weź drugą i jak żyletka przetnij prostopadle
do linii zgjęcia, wejdzie ona miedzy nie i to jest kąt liniowy kąta dwuściennego.
31 sty 22:26
Basiek : Prawdę mówiąc temat kątów w figurach przestrzennych w gimnazjum w ogóle nie był poruszany. Wzór
na objętość graniastosłupa i ew. ostrosłupa i to wszystko.
31 sty 22:27
krystek:
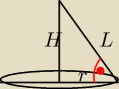
w zad masz tworzącą do pł podstawy
a czerwony to kąt nachylenia tworzącej do pł podstawy!
31 sty 22:30
krystek: to teraz rozumiesz?Basiek z Podlasia?
31 sty 22:33
31 sty 22:33
Basiek : Wybacz, bawiłam się kartkami

Tak, dużo, dużo lepiej

Jeszcze na pewno będę musiała jakoś te dwuścienne sobie no...
dopracować, ale lepiej− o niebo.
Dziękuję

. Oboje z
Agą mi zawsze tyłek ratujecie. Jestem ogromnie wdzięczna.
I nie, nie z Podlasia, z Małopolski

31 sty 22:36
Aga1:
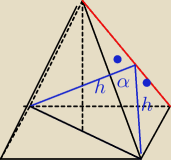
Zaznaczę Ci kąt dwuścienny między dwiema ścianami bocznymi w ostrosłupie prawidłowym
czworokątnym
31 sty 22:37
Basiek : Mhm, tu rozumiem powyżej. Tylko jedno pytanie− on jakby wychodzi z połowy tej krawędzi , tak?
Zawsze jakieś charakterystyczne punkty?

31 sty 22:40
krystek: ponieważ zestaw zad był z Olecka stąd ta sugestia .
Pozdrawiam ! I do jutra

jestem
31 sty 22:40
Basiek : Zestaw wygooglowałam

Miał odpowiedzi, opisany poziom... więc robię.
Dobranoc
Krystek, jeszcze raz dziękuję

31 sty 22:42
Basiek : Zestaw wygooglowałam

Miał odpowiedzi, opisany poziom... więc robię.
Dobranoc
Krystek, jeszcze raz dziękuję

31 sty 22:42
krystek: ramiona tego kąta (niebieskie) sa prostopadłe do krawędzi bocznej(czerwonej )
i wybieramy te które natrafiły na wierzchołki przy podstawie .( mozna by ich kreślić
nieskończenie wiele)
31 sty 22:45
Basiek : Jak to nieskończenie wiele ?

31 sty 22:51
Aga1: Dla celów obliczeniowych wystarczy tylko jeden, a te wysokości niebieskie to raczej nie są w
połowie
czerwonej krawędzi ..
Można narysować jeszcze samą ścianę boczną i wysokość poprowadzoną do ramienia tego trójkąta.
31 sty 22:57
Basiek : Okej, dziękuję Ci bardzo
Aga, za jakiś czas (tj. jutro lub pojutrze) zaczniemy już robić
całą stereometrię, więc będę mogła to wykorzystać w praktyce

Mam nadzieję, że będzie
dobrze. W razie czego mogę biec do Ciebie po pomoc?

31 sty 23:02
Aga1: Będzie dobrze..
31 sty 23:59
Basiek : Oj, musi być.

Szkoda, że stereometria jest taka czasochłonna. Postaram się radzić sobie sama

1 lut 00:01
Basiek :
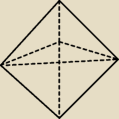
Czy ktoś może mi powiedzieć, jak nazywa się figura na rysunku? (złożona z dwóch czworościanów
foremnych?)

1 lut 19:27
Huckleberry:
zdaje sie oktaedr

1 lut 19:43
Aga1: ośmiościan(oktaedr)
1 lut 19:46
krystek: oktaedr to osiem a tutaj mamy sześć −nie znam nazwy od seksty (6) sekstader?
1 lut 19:49
krystek: Ale basiek połaczył dwa czworościany foremne i nie ma nazwy −nie jest pokazany w wielościanach
foremnych
1 lut 19:53
Aga1: Nie doczytałam, nie znam nazwy,
1 lut 19:56
1 lut 19:57
krystek: ok Eta ,ale jak trudny uczeń to efekt ?
1 lut 20:00
Eta:


1 lut 20:01
krystek: @
Eta zobaczymy czy odezwie sie . Pozdrawiam

1 lut 20:15
Eta:

hmm .... napisał,że jutro skonfrontuje z korepetytorem

1 lut 20:18
Basiek : Witajcie!
Hm, okej

Nie było mnie... ale nauczyłam się nowej nazwy − oktaedr. Od razu polubiłam

Po skonsultowaniu− pytanie brzmiało dokładnie, dlaczego tej figury powyżej nie można nazwać
sześcianem, mimo że ma 6 ścian?

1 lut 20:30
BLAZEJ_505: ja wiem

1 lut 20:31
Basiek : "Wiem, ale nie powiem!" ?

1 lut 20:31
BLAZEJ_505: dlatego że sześcian to figura, która składa się z kwadratów
1 lut 20:32
1 lut 20:34
Basiek : Z ośmiościanem się już poznałam ;> Ale dziękuję.
"wielościan foremny o sześciu ścianach w kształcie identycznych kwadratów. Posiada dwanaście
krawędzi, osiem wierzchołków i 4 przekątne. "
Czyli odpowiedź jest taka, że powyższa figura zwyczajnie nie spełnia żadnego kryterium za
wyjątkiem ilości ścian?

1 lut 20:36
Eta:
Jaki z tego wniosek ?

1 lut 20:42
Basiek : Nie jest to sześcian, a moim zdaniem... sześciościan foremny?
I ten drugi wniosek: lubię dziwne nazwy (?)

1 lut 20:44
Basiek : Witajcie

Mam kolejne pytanie: czy przekątną oktaedru wyznaczają wierzchołki dwóch czworościanów
foremnych, z których jest jakby złożona (chodzi mi o te dwa leżące naprzeciw siebie...)?
No, mam nadzieję, ze mnie rozumiecie.

4 lut 16:23
Godzio:
Tak, ale takie rzeczy masz w googlach

To jest ośmiościan foremny

4 lut 16:25
Basiek : Wiem, że to jest ośmiościan foremny, ale wolę nazwę "oktaedr"

Poza tym wygooglowanie, że
d=a
√2 jest banalne, wygooglowanie jak to obliczyć− też. Ale żeby znaleźć co ją wyznacza, to
już nie do końca

4 lut 16:34
Godzio: Jak to nie wiadomo co oznacza ? To chyba logiczne, tam jest tylko jedna główna przekątna

4 lut 16:57
Basiek : Jeśli coś wiem, to o to nie pytam. Jeśli więc zapytałam to...
* Ile płaszczyzn symetrii można poprowadzić przez każdy wierzchołek czworościanu foremnego (i
dlaczego 3?)

Ja, ignorantka, widzę 1... i niestety tylko 1.
4 lut 18:47
Basiek : Dobra, inaczej. W googlach nie znalazłam, nie oczekuję, że ktoś mi to narysuje, ale...
Czy to o to chodzi:
tak? nie?
http://i42.tinypic.com/oh8y7a.jpg
Dziękuję

4 lut 18:57
Basiek : Tak? Nie? Nie? Tak?
Ekhem...

4 lut 19:17
Basiek : up ?

4 lut 20:31
Basiek : Podstawą graniastosłupa pochyłego jest prostokąt. Każdy kąt, który tworzy krawędź boczna z
krawędziami podstawy ma miarę 60 st. Wyznacz kąt między krawędzią boczną, a płaszczyzną
podstawy.
No i nie umiem... nic, a nic. Mogłabym chociaż jakąś podpowiedź? (wiem, że nikt nie lubi
stereometrii)

4 lut 23:55
Eta:
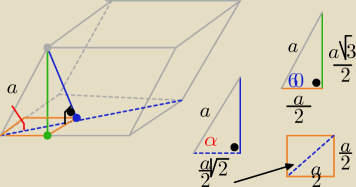
Mam nadzieję,że coś tu rozszyfrujesz

5 lut 01:08
Basiek : Ekhem.

Dzięęęękuję
 Eta
Eta
Chyba będę rozszyfrowywać, jak już będzie jasno

Ale wygląda... przejrzyście.

A już na pewno pomysłowo!

5 lut 01:12
Eta:

5 lut 01:17


 My jesteśmy bardzo mili
My jesteśmy bardzo mili 


 Tak, to jest groźba
Tak, to jest groźba 

 na zgodę
na zgodę 



 Witaj Aga
Witaj Aga 



 Nie wiem, dlaczego ktoś zakłada, że "to było i mamy umieć"...
Nie wiem, dlaczego ktoś zakłada, że "to było i mamy umieć"...
 Ja mam ferie 2 tygodnie
Ja mam ferie 2 tygodnie 
 A w ogóle, to moje ferie zaczynają się zaraz po tej maturze, w przyszły tyg, w środę, więc
przeżyję !
A w ogóle, to moje ferie zaczynają się zaraz po tej maturze, w przyszły tyg, w środę, więc
przeżyję !
 Jaką masz średnią ? ( maxa?
Jaką masz średnią ? ( maxa? 
 mam podobny dylemat
mam podobny dylemat 
 Ogólnie mam tak:
Psychologia: 4,5
Filozofia: 4
Logika: 3
Analiza: 4,5 (jutro bede oglądać prace z egz, − 18,5 / 24 −− brakuje mi 0,5 pkt do 5 bo z
ćwiczeń miałem 5 więc zobaczymy)
Algebra: 4,5 (tu mogę się pochwalić, napisałem egzamin najlepiej na kierunku, uff udało się
Ogólnie mam tak:
Psychologia: 4,5
Filozofia: 4
Logika: 3
Analiza: 4,5 (jutro bede oglądać prace z egz, − 18,5 / 24 −− brakuje mi 0,5 pkt do 5 bo z
ćwiczeń miałem 5 więc zobaczymy)
Algebra: 4,5 (tu mogę się pochwalić, napisałem egzamin najlepiej na kierunku, uff udało się  )
)

 (dzięki Trivialowi !
(dzięki Trivialowi !  )
)

 Jej, w koło sami mądrzy ludzie
Jej, w koło sami mądrzy ludzie 
 ( echch ta logika !
( echch ta logika ! 


 i odpytka była, ale
odpowiedziałem na wszystko więc jest ok
i odpytka była, ale
odpowiedziałem na wszystko więc jest ok  No ale trudno
No ale trudno 







 W każdym razie w dodawaniu się pomyliłem
W każdym razie w dodawaniu się pomyliłem


 No po prostu, to jest dla mnie całkiem naturalne...
I fakt faktem dla mnie pole boczne to chyba powinno być całe pole powierzchni bocznej..., ale
nie będę się sprzeczać. Wychodzi.
No po prostu, to jest dla mnie całkiem naturalne...
I fakt faktem dla mnie pole boczne to chyba powinno być całe pole powierzchni bocznej..., ale
nie będę się sprzeczać. Wychodzi.  Dziękuję
Dziękuję 
 !
!


 Nie umiem,
Nie umiem,
 ten czerwony to kat między ściana boczna a pł podst.
ten czerwony to kat między ściana boczna a pł podst.

 2)Przekrój osiowy walca jest prostokątem o wymiarach h na 2r.
Przekątna przekroju, to przekątna prostokąta
2)Przekrój osiowy walca jest prostokątem o wymiarach h na 2r.
Przekątna przekroju, to przekątna prostokąta


 w zad masz tworzącą do pł podstawy
a czerwony to kąt nachylenia tworzącej do pł podstawy!
w zad masz tworzącą do pł podstawy
a czerwony to kąt nachylenia tworzącej do pł podstawy!

 Tak, dużo, dużo lepiej
Tak, dużo, dużo lepiej  Jeszcze na pewno będę musiała jakoś te dwuścienne sobie no...
dopracować, ale lepiej− o niebo.
Dziękuję
Jeszcze na pewno będę musiała jakoś te dwuścienne sobie no...
dopracować, ale lepiej− o niebo.
Dziękuję  . Oboje z Agą mi zawsze tyłek ratujecie. Jestem ogromnie wdzięczna.
I nie, nie z Podlasia, z Małopolski
. Oboje z Agą mi zawsze tyłek ratujecie. Jestem ogromnie wdzięczna.
I nie, nie z Podlasia, z Małopolski 
 Zaznaczę Ci kąt dwuścienny między dwiema ścianami bocznymi w ostrosłupie prawidłowym
czworokątnym
Zaznaczę Ci kąt dwuścienny między dwiema ścianami bocznymi w ostrosłupie prawidłowym
czworokątnym

 jestem
jestem
 Miał odpowiedzi, opisany poziom... więc robię.
Dobranoc Krystek, jeszcze raz dziękuję
Miał odpowiedzi, opisany poziom... więc robię.
Dobranoc Krystek, jeszcze raz dziękuję 
 Miał odpowiedzi, opisany poziom... więc robię.
Dobranoc Krystek, jeszcze raz dziękuję
Miał odpowiedzi, opisany poziom... więc robię.
Dobranoc Krystek, jeszcze raz dziękuję 

 Mam nadzieję, że będzie
dobrze. W razie czego mogę biec do Ciebie po pomoc?
Mam nadzieję, że będzie
dobrze. W razie czego mogę biec do Ciebie po pomoc? 
 Szkoda, że stereometria jest taka czasochłonna. Postaram się radzić sobie sama
Szkoda, że stereometria jest taka czasochłonna. Postaram się radzić sobie sama 
 Czy ktoś może mi powiedzieć, jak nazywa się figura na rysunku? (złożona z dwóch czworościanów
foremnych?)
Czy ktoś może mi powiedzieć, jak nazywa się figura na rysunku? (złożona z dwóch czworościanów
foremnych?) 

 Wytłumaczcie , bo ja nie mam już siły
Wytłumaczcie , bo ja nie mam już siły  https://matematykaszkolna.pl/forum/124934.html
https://matematykaszkolna.pl/forum/124934.html



 hmm .... napisał,że jutro skonfrontuje z korepetytorem
hmm .... napisał,że jutro skonfrontuje z korepetytorem 
 Nie było mnie... ale nauczyłam się nowej nazwy − oktaedr. Od razu polubiłam
Nie było mnie... ale nauczyłam się nowej nazwy − oktaedr. Od razu polubiłam  Po skonsultowaniu− pytanie brzmiało dokładnie, dlaczego tej figury powyżej nie można nazwać
sześcianem, mimo że ma 6 ścian?
Po skonsultowaniu− pytanie brzmiało dokładnie, dlaczego tej figury powyżej nie można nazwać
sześcianem, mimo że ma 6 ścian? 





 Mam kolejne pytanie: czy przekątną oktaedru wyznaczają wierzchołki dwóch czworościanów
foremnych, z których jest jakby złożona (chodzi mi o te dwa leżące naprzeciw siebie...)?
No, mam nadzieję, ze mnie rozumiecie.
Mam kolejne pytanie: czy przekątną oktaedru wyznaczają wierzchołki dwóch czworościanów
foremnych, z których jest jakby złożona (chodzi mi o te dwa leżące naprzeciw siebie...)?
No, mam nadzieję, ze mnie rozumiecie. 
 To jest ośmiościan foremny
To jest ośmiościan foremny 
 Poza tym wygooglowanie, że
d=a√2 jest banalne, wygooglowanie jak to obliczyć− też. Ale żeby znaleźć co ją wyznacza, to
już nie do końca
Poza tym wygooglowanie, że
d=a√2 jest banalne, wygooglowanie jak to obliczyć− też. Ale żeby znaleźć co ją wyznacza, to
już nie do końca 

 Ja, ignorantka, widzę 1... i niestety tylko 1.
Ja, ignorantka, widzę 1... i niestety tylko 1.




 Mam nadzieję,że coś tu rozszyfrujesz
Mam nadzieję,że coś tu rozszyfrujesz
 Dzięęęękuję
Dzięęęękuję  Eta
Chyba będę rozszyfrowywać, jak już będzie jasno
Eta
Chyba będę rozszyfrowywać, jak już będzie jasno  Ale wygląda... przejrzyście.
Ale wygląda... przejrzyście.  A już na pewno pomysłowo!
A już na pewno pomysłowo! 
