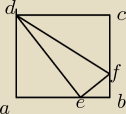
planimetria zbk: W kwadrat ABCD o boku mającym długość 10 cm wpisano trójkąt równoramienny DEF, |DE|=|DF|, w taki sposób, że E należy do AB i F należy do CB. Wiedząc, że pole trojkata DEF jest rowne 18cm², oblicz sin|kąta EDF|.

Eta:

	9
sin∡EDF=
	41

zbk: A MOZNA JAKIES WSKAZÓWKI BO NIE WIEM JAK DO TEGO DOJŚĆ bardzo prosze

Eta:

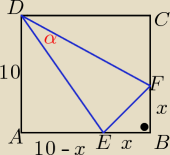
	|DE|2		36
PΔ(EFD)=		*sinα ⇒ sinα=
	2		|DE|2

P kwadratu −( 2*PΔAED +PΔEBF)= PΔEFD

	1
100 −(10*(10−x)+		x2)= 18 , x € (0, 10)
	2

|DE|²= .......... z tw. Pitagorasa powodzenia

zbk: teraz juz sobie poradze sin wyznaczylem z wzoru na pole lecz nie domyslilem sie zeby potem w ten sposób wielkie dzieki

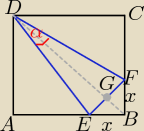
Eta: 2/ sposób czworokąt ABFD jest deltoidem o przekątnych długości : |BD|= 10√2 i |EF|= x√2

	10√2*x√2		1
P(deltoidu) =		= 10x , P (ΔEFB)=		x2 , x€ (0,10)
	2		2

P(deltoidu − P(ΔEFB)= 18 otrzymasz równanie kwadratowe z "x" ........... rozwiąż to równanie dla x€ (0,10) i dalej podobnie jak w 1 sposobie

Eta: poprawiam chochlika : czworokąt EBFD jest deltoidem

Kasia:

	1
A czy Eta w 1. sposobie nie zgubila w nawiasie		? tam gdzie sie zaczyna od 100 − .....
	2

to w nawiasie z poczatku powinien byc jeszcze 1/2 chyba, bo wzor na pole to a*h/2 , czyz nie?

Kasia: sorry, cooofam, zapomnialam,ze tam jest *2 przez co sie wyrownuje nie bylo pytania

Kasia: jednak mam pytanie, ile powinno byc DE? bo cos mi sie chyba nie zgadza..

Amator: Mi DE wyszło √164 sin ¹⁸_2√41

Carolinga: A czy sinα nie powinien wyjść 9/41? Bo że wzoru na sinusa jest sinα= 36/DE² więc tam pierwiastek się zeruje i zostaje 36/164