zadanie Kasia: Mała rozgrzewka. Zarzuci ktoś jakimś zadankiem na poziomie liceum + poziom podstawowy? taka mała powtóreczka przed maturką

elpe: cosx−√3sinx=1

Kasia: po pierwsze jaka jest treść zadania? i czy to aby na pewno p. podstawowy?

ICSP: to nie jest poziom podstawowy Na pewno xD Przekątna kwadratu jest o √2 dłuższa od jego boku. Oblicz bok kwadratu

Kasia: d = a√2 d = a + √2 a+√2 = a√2 a√2 − a = √2 a(√2−1} = √2

	√2		√2(√2+1)
a =		=		= 2 + √2
	√2−1		2−1

ICSP:

Kasia: robiłam to zadanie chyba w tą sobote nawet xDD pamiętałeś czy tak przypadkiem dałeś?

ICSP: wykaż że prawdziwy jest wzór : sin²x + cos²x = 1

chcesieuczyc: ech chyba tez sie zaczne z wami przygotowywac z matmy poprzez rozwiazywanie zadan

Kasia: e no, teraz to już przesadziłeś podano mi taką własność w szkole, ale nikt mi nie tłumaczył skąd to się wzięło

ICSP: narysuj trójkąt. Oznacz w nim kąt α. Zapisz długości boków jako jakieś literki. I podstaw te literki do wzoru xD

Też chcę inny nick! : Spróbuj może z tangensów/ cotangensów?

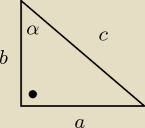
Kasia: i w czym mi to ma niby pomóc? bo jakoś dalej nie widzę, żeby z tego mógł wyjść jakiś dowód, ale ok.. narysuje Ci piękny trójkąt : P sin²x + cos² x = 1

	a		b
(		)2 + (		)2 = 1
	c		c

a2		b2
	+		= 1
c2		c2

a2+b2
	= 1
c2

pytanie: co w tym przypadku jest tym 'x'? bo mi go chyba brakuje, i mógłby w czymś pomóc.. xD

ICSP: x to α Dokończ dowód.

Kasia: hm.

a2α + b2α
	= 1
c2α

a2α+ b2
	= 1
c2

nie mam pomysłu..

ICSP: skoro a = x to

	a
sinx =
	c

	b
cosx =
	c

x już zniknęły. Teraz działasz na samych literkach

a2 + b2
	= 1
c2

musisz to udowodnić i nawet nie mów że nie wiesz.

Kasia: nie wiem czy to dobry tok rozumowania, ale na razie nic innego nie przyszło mi do głowy. a² +b² = c² ⇒ trójkąt jest prostokątny, zgodnie z twierdzeniem Pitagorasa. chociaż to moim zdaniem w ogóle nie udowadnia tamtej własności, no ale cóż..

ICSP: no i właśnie tutaj trzeba skorzystać z twierdzenie Pitagorasa . Masz

a2 + b2		c2
	=		= 1
c2		c2

c.n.u. Teraz udowodnij :

	sinx
tgx =
	cosx

Kejt: teoretycznie zgodnie z twierdzeniem odwrotnym do tw. Pitagorasa..przynajmniej wg mnie. wybaczcie, że się Wam wtrącam

BLAZEJ_505: tak dobrze rozumiesz teraz jak podstawisz c²=a²+b² do wzoru ^a2+b2_c² =1 to co wyjdzie ? polecam filmik http://www.youtube.com/watch?v=1l5FydhO7bk

ICSP: Witaj Kejt Miło że się wtrąciłaś Wiem ze miałaś mi podać rozwiązanie (sin² 20^o * sin² 40^o * sin² 60^o * sin² 80^o )

Kejt: <znika w tajemniczych okolicznościach>

Kasia: już robie

ICSP: no dobra nie będę ciebie dłużej meczył. Skorzystaj z tego że : 4 * sin(60−α) * sinα * sin(60+α) = sin3α

Kasia: ok. rysunek ten sam.

	sinα
tgα =
	cosα

	a
sinα =
	c

	b
cosα =
	c

	a
L = tgα =
	b

	sinα		a/c		a		c		a
P =		=		=		*		=
	cosα		b/c		c		b		b

L = P C.N.U ^

ICSP: Dobrze to masz już opanowane Nie chcesz rozwiązać zadania dla Kejt

Kejt: śmiało..ja nadal nie wiem o co chodzi..

Kasia: NIE NIE NIE NIE ! ! ! ! jak takie zadania masz mi dawać, to ja może pójdę..

ICSP: nawet jak ci podałem tą tożsamość ?

ICSP: Pytałem tylko Z jakiego działu chcesz?

Kasia: moja odwiedz brzmi : nie dziękuję. Kejt: życzę natchnienia i cierpliwości... : P hmm.. może f. wykładnicza albo wymierna, bo już trochę czasu minęło od mojej ostatniej styczności z nimi ...

ICSP: no to : rozwiąż nierówność : 3^x > 0

Kejt: ile powinno wyjść?

Kasia: nieskończenie wiele rozwiązań?

ICSP: w którym?

ICSP: Kasiu zapisz to jakoś tak rozsądnie

Kejt: w tym moim..wyszedł mi trochę dziwny ułamek..

Kasia: no, ale na logike odrazu widać ale gdybym to miała jakoś udowodnić, to bym napisała po prostu , że : kiedy x = 0 ⇒ 3⁰ = 1 , co jest większe od 0 i dla każdej liczby x dodatniej bądz ujemniej 3 do danej potęgi, będzie liczbą dodatnią, większą od 0.

ICSP:

9
256

ICSP: wiem ze od razu widać. Tylko chodzi o ładny zapis Szukamy x więc x = ?

Kejt: ja bym napisała po prostu x∊lR wyszedł mi trochę inny..liczę dalej..

ICSP: no i dobrze byś napisała

Kasia: aaa, o to Ci po prostu chodzi x ∊ ℛ

gauspn: x∊<0;∞)

ICSP: tak teraz dobrze

Kasia: nieprawda, bo ujemne liczby tez naleza do przedzialu, wiec po prostu R...

ICSP: teraz Kasiu dam ci coś na zabicie czasu bo będę musiał iść rozwiąż w liczbach rzeczywistych równanie : x³ + 3x² + 3x + 11 = 0

Kasia: x = −³√10 − 1 tak można po prostu zostawić?

Eta:

Kasia: jakieś jedno zadanko na dobranoc? tym razem już ja chcę zrobić od a do z !

Kasia: hahaha, dzięki Kejt za wsparcie

Kasia: i poprawka : dotarłyście * wybaczcie

Kejt: nie ma sprawy, imienniczko lecę spać, dobranoc.

gauspn: Oblicz a⁴+b⁴ jeśli, a²+b²=2 i ab=1

Kasia: kolorowych snów !

ICSP: Eta czy przypadkiem z tego tematu nie zniknęło kilka postów?

Eta: a⁴+b⁴= (a²+b²)²−2a²b²=(a²+b²)²−2(ab)²=............ dokończ

Kasia: Eta Jesteś wielka! haha

Eta: Jakich postów ? ICSP

gauspn: Nie no tak się wtrąciłem do tematu bo miało to być zadanie dla Kasi, jeżeli bym chiał żeby mi ktos rozwiązał to bym założył nowy temat

Kasia: Eta: już dokończe, sekundka

Eta: Sorry na przyszłość pisz: tylko dla Kasi !

gauspn: Ja to troche inaczej zapisałem a mianowaicie: (a²+b²)²=a⁴+2a²b²+b⁴ (a²+b²)²=a⁴+2(ab)²+b⁴ 2²=a⁴+b⁴+2(1)² 4=a⁴+b⁴+2 4−2=a⁴+b⁴ 2=a⁴+b⁴ a⁴+b⁴=2

Kasia: po 1) ICSP, nie gniewaj się na nich, one mi uprzejmie pomogły, bo sama i tak bym na to nie wpadła.. po 2) dzięki gauspn, widzę, że nie mam po co pisać już, a już bym sobie naprawdę z tym poradziła.. eh..

Kasia: na nie* , nie mam co ja mam dzisiaj z tym rodzajem męskim..

Kasia: nie wiem co ja mam*

ICSP: na nikogo się nie gniewam przecież Ja jestem dla wszystkich bardzo miły

Eta: >

Matura!12: jak tak patrze na te zadania.. to masakra. Nie wiem czay zdam matme Chyba wybiore sie na korki