1/(1+x^2)^2 Grimm:

	1
∫		dx
	(1+x2)2

Liczę i liczę i się nie doliczę. Jak to rozwiązać? To przykładowe zadanie na egzamin 1 roku więc powinna być jakaś prosta metoda.

bart:

	1
rozbij na dwa ulamki i skorzystaj ze wzoru ∫		=arctgx+C
	1+x2

Grimm: Kwadrat wszystko psuje

bart: dlatego rozbij to na dwa ulamki o mianowniku 1+x²

bart: albo i wiecej

ZKS: x = tgu dx = (tg²u + 1)dt

	1		dt
∫		* (tg2u + 1)dt = ∫		dt =
	(1 + tg2u)2		1 + tg2u

	cos2u + sin2u		1
1 + tg2u =		=
	cos2u		cos2u

	sinucosu		u
= ∫ cos2u dt =		+		+ C =
	2		2

	sin(arctg(x))cos(arctg(x))		arctg(x)
=		+		+ C
	2		2

Trivial:

ZKS: To dzięki Tobie Trivial bo pokazałeś tą metodę i napisałem na maxa całki. Jeszcze raz dziękuję.

Trivial:

	x
tgu =		= x
	1

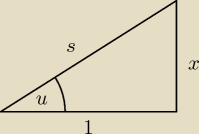
	x		x
Zatem sinu =		=
	s		√x2+1

	1		1
cosu =		=
	s		√x+1

	x
sinucosu =		.
	x2+1

Trivial: Gratulacje.

ZKS: Oo to będę musiał zobaczyć bo ciekawe.

ZKS: Dziękuję za gratulację i za metodę z podstawieniem trygonometrycznym.

Grimm: Przyznam że sposób jest bardzo fajny Choć znając życie jest inny tak genialnie prosty że żadne z nas go nie widzi jeszcze Tak czy siak dzięki wielkie za pomoc

Trivial: Jest sposób rekurencyjny. https://matematykaszkolna.pl/forum/121374.html

ZKS: Jeżeli ten nie jest bardzo prosty to ja już nie wiem jakie to są proste. Chyba te które od razu można policzyć ze wzoru.

Grimm: Jest prosty, nie mówię, że nie I fajny bo sprytny.