Planimetria ...: Witam. Potrzebuję pomocy, mam klopoty z planimetrią... W trójkącie ABC dane są AB=7cm, AC=6cm, BC=5cm. Wiadomo, ze boki AC i BC są styczne do okręgu którego środek leży na boku AB. Znajdź dlugość promienia okręgu.

...: próbowalem wykorzystać tw. o dwusiecznej kąta wewnętrznego, niestety nie wiem co dalej...?

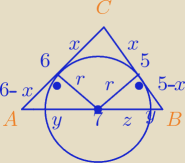
Godzio: Narazie nie widzę ciekawego rozwiązania, ale rozwiązując ten układ: r² + (6 − x)² = y² r² + (5 − x)² = z² y + z = 7 otrzymasz je

Godzio: W sumie nie ... 4 niewiadome 3 równania bez sensu

ICSP: r,x,y,z trzy równania cztery niewiadome?

ICSP: może być coś kminic z wysokością która jest równoległa do r.

...: do tego to i ja doszedlem jakoś nie mam pomyslu... Próbowalem też tw. cosinusów zastosowac i owszem można by bylo policzyć, ale to zawsze dziwne wyniki wychodza

al: albo pole policzyć z Herona, a potem z dwóch trójkątów o wysokości r i podstawach 6 i 5.

al:

	12√6
wyszło mi r=
	11

...: Zapisz początek, bo nie bardzo wiem jak przyrównaleś?

al: z Herona pole wyszło 6√6=1/2*6*r+1/2*5*r

pigor: no cóż , ja mam zwyczaj podać "mojego" gotowca − nie gotowca, a reszta jest ... milczeniem, czyli należy do ciebie, oczywiście wszyscy inni chętni mogą ci ... pomagać, proszę bardzo , ale mi jest na to ... niestety , albo stety szkoda czasu, a więc np. taki gotowiec niech r=? − szukany promień , to z warunków zadania, tw. o stycznej do okręgu i tw. Pitagorasa : r²+(6−x)²=r²+(5−x)²=3,5² ⇒ ... (6−x)²−(5−x)² = 0 ⇔ (6−x−5+x)(6−x+5−x) = 0 ⇔ 2x=11 ⇔ x=5,5 , zatem np. r²+(6−5,5)²=3,5² ⇔ r² = 3,5²−0,5² ⇔ r² = 3 * 4 i r >0 ⇒ r=2√3 . ...

pigor: niestety mam złe założenie, będę myślał dalej , a więc wynik zły , przepraszam za TAKI gotowiec ...

...: sam muszę nad tym pomyśleć jeszcze, a jak na nic nie wpadne to looknę na te wasze hieroglify. Z Herona wlasnie wcześniej chcialem skorzystać, ale nie bardzo wiedzialem jak za pomocą innego wzoru otrzymac szukane r. Mam jeszcze jedno zadanie: Dwa okręgi o r1=3cm 22=9m są styczne zewnętrznie. Oblicz pole oraz obwód figury ograniczonej tymi okręgami i ich wspólną styczną zewnętrzną. Prosilbym o rysunek, bo nie wiem jak to wgl. ma wyglądać..

wolf:

	6√6
r=
	11

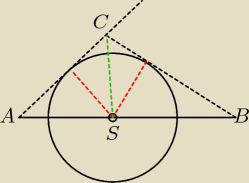
Bizon: Rysunek troszkę odwrócony ... ale zrobisz lepszy −

6		5		7
	=		=
sinα		sinβ		sinγ

Wykorzystując twierdzenie sinusów policzysz w jakiej proporcji podzielone są boki ... ... a dalej już ...

...:

	2√6
Obliczylem pole z Herona wyszlo te 6√6. 6√6=pr => r=
	3

pigor: dlatego nowy ... gotowiec np. taki ¹₂ * 5 *6sinα =¹₂ * 5r+¹₂* 6r , czyli r=sinα = ? , no to z tw. cosinusów

	62+52−72
cosα =		= ... = 15 >0 ⇒ sin2α = 2425 ⇒
	2*6*5

	2√6		2√6
sinα =		, zatem ... r=
	5		5

Bizon:

r
	=sinα
IASI

r
	=sinβ ... itd
IBSI

...: dobra, dobra, starczy Narysujcie mi jeszcze to co podane jest w zadaniu kilka postów wcześniej

pigor: źle , znowu źle coś chyba w rachunkach idę strzelić sobie piwa , to prze tego brak podglądu online , . ...

al: pole ΔABC=poleΔACS+poleΔCSB

pigor: ... już wiem

	30		30		1		6
r =		* sinα =		*		=		i KONIEC wreszcie
	11		11		5		11

pigor: no jak na dzisiaj to za dużo ...

...: Patrzę to samo macie co ja. Jak mi nie wychodzi to się wkurzam i wracam do tego aż w końcu wyjdzie ewentualnie rzucam tutaj, ale rzadko jakoś znajdują się chętni do pomocy ostatnimi czasy

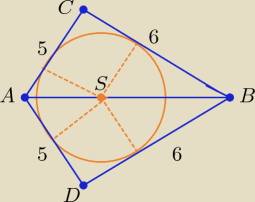
wolf: Dokończę ( bez piwa |AC|= 5 r −−− jest promieniem okręgu wpisanego w deltoid ABCD

	Pdeltoidu
r=
	0,5 obwodu deltoidu

P= 2P ΔABC= ......... z Herona = 12√6 0,5 obwodu deltoidu = 11

	12√6
r=
	11

Wynik podany przez al jest poprawny ( mnie zgubiła się poprzednio dwójka z pola)

Mila: Prawidłowe rozwiązanie Ala!.

wolf:

...: dzięki wielkie. Mogę jeszcze o rysunek do tego zadania prosić? Dwa okręgi o r1=3cm 22=9m są styczne zewnętrznie. Oblicz pole oraz obwód figury ograniczonej tymi okręgami i ich wspólną styczną zewnętrzną.

Bizon:

25√3
22

pigor: ... :ale mi się popieprzyło , przez ten "głupi" edytor,

	30		30		2√6		12
r=		* sinα =		*		=		√6 ≈ 2,61 . ...
	11		11		5		11

wolf: A może przez

pigor: o, to TEZ i ostatni raz dałem się wciągnąć w taki wyścig ... forumowych szczurków , pozdrawiam ...

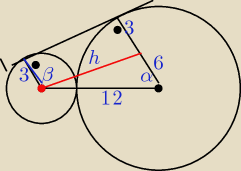
Aga1: α=60⁰ Chyba już będzie jasne.

...: o teraz tak pigor nie zrażaj się tak latwo do "wyscigu forumowych szczurków"

pigor: nie, po prostu, będę chodził swoim ... rytmem , pozdrawiam

...: Mam pytanie do takiego zadania: Wysokość i środkowa poprowadzone z jednego wierzcholka kąta trójkąta dzielą ten kąt na trzy równe części. oblicz kąty trójkąta. Czy jeżeli dziela na trzy równe części kąt to i podstawę na trzy odcinki równej dlugości?

Mila: Podstawy nie!

...: o to chyba będzie ciężko

Mila: Nie jest to zbyt trudne zadanie . Było na kółku w gimnazjum.

...: to fakt, bylo proste