Takie tam różne.
Basiek: Takie tam różne. Pomocy?
Mam serię pytań do takiej kartki z zadaniami.

Więc f(x)=Ix−3I+1 g(x)=f(4−x)=> g(x)= ..... Jaki ma wzór? Nie mam pojęcia, czy tam gdzieś
nawias, czego się ten minus tyczy itd. Możecie?
29 sty 19:22
krystek: g(x)=I(4−x)−3I+1
29 sty 19:24
Aga1: g(x)=I4−x−3I+1=
patrzysz na wzór f i zamiast x wstawiasz 4−x.
29 sty 19:25
rumpek:
f(x) = |x − 3| + 1
g(x) = f(4 − x) ⇒ f(4 − x) = |4 − x − 3| + 1 = ....
29 sty 19:25
wolf:
g(x)= |4−x−3|+1=.........
29 sty 19:27
Basiek: No widzicie. Jasno, pięknie, cudownie.

Dziękuję

Czyli argumentem jest (4−x) zamiast x.
29 sty 19:27
wolf:
Ale "wysyp"

29 sty 19:28
Basiek: Miło mi z powodu tego "wysypu"


29 sty 19:29
krystek: Rzucamy się na zadania −jak zwierzęta na żer w okresie mrożnej zimy!
29 sty 19:30
wolf:


29 sty 19:32
Basiek: Właśnie widzę tę kartkę... i już wiem, że będę mogła Wam dostarczyć rozrywki!

29 sty 19:35
krystek: 
29 sty 19:38
Basiek: Może coś ze mną nie tak, ale zrobiłam masę zadań, a takich nie widziałam O
o
| | 2−n | |
a) zbadaj monotoniczność ciągu an= |
| cos(nπ) |
| | n | |
29 sty 19:47
ZKS:
Ten ciąg nie jest monotoniczny.
29 sty 19:59
Basiek: ZKS a coś więcej? Bo normalnie to byłoby a
n− a
n−1=....
ale ten cos(nπ)... to przekracza moje możliwości

29 sty 20:02
wolf:
wskazówka cosπ*n= (−1)n = −1 lub 1
zbadaj różnicę dla n parzystego i n nieparzystego
an+1−an =..........
29 sty 20:03
ZKS:
Hmm ciężko mi to jakoś logicznie wyjaśnić ale cos(nπ) dla n nieparzystych jest równy −1 zaś dla
n parzystych jest równy 1.
29 sty 20:04
Basiek: czyli hm, czy mogę... wyliczając popodstawiać sobie to 1 lub −1 zamiast cos(nπ)?

29 sty 20:07
ZKS:
Dla n parzystego będziesz miała
a dla n nieparzystego
29 sty 20:09
Basiek: | | 4 | |
Tak sobie właśnie zrobiłam! Rozumiem.  wyszło mi ostatecznie, że a n −a n−1= 2− |
| |
| | n | |
czyli wiadomo... niemonotoniczny

29 sty 20:10
Aga1: Jeśli stwierdzasz, że ciąg nie jest monotoniczny, to wystarczy policzyć np.
Stosowny komentarz i już.
29 sty 20:20
Basiek: Nie sądzę, żeby coś takiego przy tablicy dało mi cokolwiek
Aga , ale dziękuję

29 sty 20:21
Basiek: Dobra, w tym pierwszy policzyłam jeszcze raz, bo oczywiście wcześniej wyszły mi głupoty.
| | −n2+n−6 | |
an− an−1= |
| <− niemonotoniczny |
| | n(n−1) | |
i jest jeszcze przykład b
b
n= a
2n
| | 2−2n | |
i wyszło mi bn− bn−1= |
| więc też niemonotoniczny... |
| | 2n | |
29 sty 20:40
Aga1: Aby stwierdzić, że ciąg nie jest rosnący, ani malejący, wystarczy zauważyć , na przykład, że
piąty wyraz jest większy od szóstego, natomiast szósty mniejszy od siódmego.
a6<a5
a7>a6
Musisz korzystać z definicji , jeśli chcesz udowodnić monotoniczność ciągu.
29 sty 20:40
Basiek: No, ale na tej podstawie przecież an− an−1=.... widzimy, że ta rożnica to zmienna, tak?
Przyjmuje wartości zarówno ujemne, jak i dodatnie... więc ciag nie może być monotoniczny.
29 sty 20:42
Aga1: Wydaje się, że obydwa sposoby są do zaakceptowania.
29 sty 20:57
Basiek: A coś takiego?
Miara największego kąta w trójkącie jest dwa razy większa od miary najmniejszego kąta. Oblicz
długość boków tego trójkąta, jeśli są one kolejnymi liczbami naturalnymi.
Może chociaż jakiś pomysł? Oznaczyłam sobie to... i liczyłam niby z tw, cos, ale wyszło mi tyle
zmiennych itd...
29 sty 21:05
Aga1:
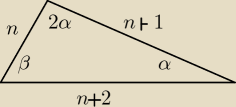
29 sty 21:15
Basiek: β ma u mnie 180−3α , ale reszta tak samo. Tylko nie wiem, co dalej

29 sty 21:15
Aga1: Liczyłaś z tw. cosinusów i nie wyszło?
29 sty 21:17
Basiek: doszłam do postaci
a2+6a+5=(2a2+6a+4)cosα
29 sty 21:19
Aga1: Dwa razy tw. cosinusów i tw. sinusów
Ale , czy nie da się zrobić tego zadania prościej?
29 sty 21:27
Ania: | | n | | n+2 | | n+2 | | n+2 | |
robiłam to zad ostatnio  |
| = |
| n= |
| cosα = |
| |
| | sinα | | sin2α | | 2cosα | | 2n | |
teraz z tw cos do kąta α

29 sty 21:31
Basiek: Aniu dzięki, Aga Tobie też.
W sumie wyszło mi coś sprzecznego z tego..., ale nie mam siły się z tym użerać. Pokonała mnie
ta śmieszna karteczka.
PS. Aniu, nie wiesz może skąd są te zadania? Tzn. z jakiej książki?
29 sty 21:46
Ania: tak, z "Matura z matematyki od roku 2010" zakres rozszerzony

29 sty 21:49
Basiek: A wydawnictwo jakie?

29 sty 21:51
Ania: Podkowa

29 sty 21:52
Basiek: Na pewno nie

Mam ją. Musi być z czegoś innego.
29 sty 21:58
Ania: to może z innej ale ja to zadanie mam w tej książce , str 147 zad 7.48.

29 sty 22:00
Basiek: Faktycznie

Dzięki, to sobie przeglądnę to rozwiązanie, bo jest doprowadzone do końca.
Dziękuję.

29 sty 22:02
Ania: 
29 sty 22:03
Basiek: No nic, dziękuję wszystkim

dobranoc

29 sty 22:52
 Więc f(x)=Ix−3I+1 g(x)=f(4−x)=> g(x)= ..... Jaki ma wzór? Nie mam pojęcia, czy tam gdzieś
nawias, czego się ten minus tyczy itd. Możecie?
Więc f(x)=Ix−3I+1 g(x)=f(4−x)=> g(x)= ..... Jaki ma wzór? Nie mam pojęcia, czy tam gdzieś
nawias, czego się ten minus tyczy itd. Możecie?
 Dziękuję
Dziękuję  Czyli argumentem jest (4−x) zamiast x.
Czyli argumentem jest (4−x) zamiast x.









 wyszło mi ostatecznie, że an −an−1= 2−
wyszło mi ostatecznie, że an −an−1= 2−

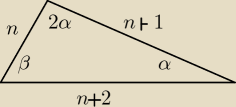






 Mam ją. Musi być z czegoś innego.
Mam ją. Musi być z czegoś innego.

 Dzięki, to sobie przeglądnę to rozwiązanie, bo jest doprowadzone do końca.
Dziękuję.
Dzięki, to sobie przeglądnę to rozwiązanie, bo jest doprowadzone do końca.
Dziękuję. 

 dobranoc
dobranoc 