Planimetria XYZ: W trójkącie ABC poprowadzono wysokość CD. Wiadomo, że punkt D leży na symetralnej boku BC, |AC| =5, |CD|=4. Uzasadnij, że długość promienia Wpisanego w trójkąt ABC jest równa 3 − √2

XYZ: Jest ktoś w stanie mi pomóc ?

wmboczek: TAK

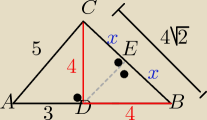
wmboczek: ADC jest prostokątny i AD=3 E − środek BC, DEC też prostokątny i x=CE Dla DEC mamy 4²=x²+DE² ⇒DE=√16−x² Dla DEB mamy √16−x²²+x²=4=DB CB²=4²+4² ⇒ CB=4√2 teraz zostaje tylko policzyć ze wzoru r=CD*AB/(AB+AC+BC)

XYZ: Dzięki

pigor: ... no to z warunków zadania, własności symetralnej boku trójkąta mam rozwiązanie prawie w ... jednej linijce takie : ze wzoru na długość promienia r okręgu wpisanego w Δ (... patrz np. tablice) mam kolejno

	S		12(3+4) *4		7 *4		7
r =		=		=		=
	p		12 (7+5+4√2)		4(3+√2)		3+√2

	7(3−√2)		7(3−√2)		7(3−√2)
=		=		=		= 3−√2 . ...
	(3+√2)(3−√2)		9−2		7

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− P.S. co niektórzy zarzucają mi , że piszę gotowce , z czym się nie zgadzam , a oto jeden z nich proszę bardzo , ...

wolf:

	7*4		7+5+4√2
P=		=14 p=		= 6+2√2
	2		2

	P		7
r=		=		= 3−√2
	p		3+√2

XYZ: Dzięki