Pomocy! zbadaj w zależności od parametru k wzajemne połozenie prostych: aqlec: Pomocy! zbadaj w zależności od parametru k wzajemne połozenie prostych: l1: kx+y=2 l2: x+ky=k+1

aqlec: jak mam to zrobić?

wolf: l₁: y= −kx+2 a₁= −k

	1		1		1
l2: y= −		+1+		, k≠0 a2= −
	k		k		k

	−1
dla a1=a2 ⇒ l1 ∥ l2 ⇒ −k=		⇒ k2= 1 ⇒ k=1 v k= −1
	k

dla k= 1 l₁: y= − x+2 l₂: y= −x +2 ⇒ proste są równoległe i pokrywają się dla k= −1 l₁: y= x+2 l₂: y= x ⇒ proste równoległe i się nie pokrywają dla k∊ R{0, −1, 1} −−−− proste przecinające się

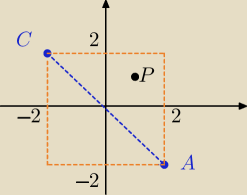
aqlec: Dziękuję! a jak zrobić to: dla jakich k te proste przecinajaą sie wewnątrz kwadratu w którym punkty a=(2,−2) i C=(−2,2) są końcami przekątnej?

Kingaa: Czy mogę ponowić pytanie aglec ? Jak zrobić drugą część zadania?

ite: Dla k=0 również mamy proste przecinające się. Czyli przecinają się dla k∊ R\{−1, 1}. Oblicz współrzędne punktu przecięcia się tych prostych P(x_P,y_P), rozwiązując ten układ równań dla podanego wyżej k. Punkt P będzie należał do wnętrza kwadratu jeśli będą spełnione warunki:

⎧	−2<xP<2
⎩	−2<yP<2

Kingaa: Dziękuję za odpowiedź