Cięciwa i okrąg Marek19: Na okręgu o promieniu r dane są punkty A , B , C i znane są długości AC=b BC=a . Jaka jest długość cięciwy AB ?

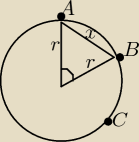
Jolanta: AC=b BC=a AB=b−a

	α
L ł =		*2πr wzór na długośc łuku
	3600

AB=Lł

α		AB
	=
3600		2πr

	AB
α=		*3600 AB masz r masz liczysz kąt
	2πr

promienie to ramiona trójkąta równoramiennego długośc cieciwy to trzeci bok obliczymy z tw,cosinusów x²=r²+r²−2*r*r*cosα /√ obustronnie i masz cieciwę

Aga1: AB=b−a − jak to Jolu wyliczyłaś?

Jolanta: W tresci zadania jest ,ze znane sa długości AC=b BC=a AB+BC=AC AB=AC−BC=b−a

Aga1: W trójkącie ABC AC≠AB+BC. Suma wektorów AB i BC jest równa wektorowi AC.

Bizon: Porównaj Jolu to co piszesz ze swoim rysunkiem

Jolanta: Zle to zrozumiąłam ? AB ,AC .BC to nie długości łuku?

Zen64: Wystarczy poprostu rozwiązać na c układ równań:

⎧	sinγ=c2r
⎩	cosγ=a2+b2−c22ab

(γ,c−niewiadome) Jak wyrugujesz uprzywilejowaną prostytutkę tv,mającą między innymi nieformalne techniczne możliwości"zaciemniania" zapisu to można się zastanowić nad sprawnością rozwiązywania powyższego układu