przebieg zbieżności.
GoodYou : 1. Zbadaj przebieg zbieżności funkcji: x2+x+1/x2−1
2.Najmniejsza i najwieksza wartość w danym przedziale. f(x)=x3−3x <−2,4>
W tym drugim stanąłem na ekstremach, bo nie wiem czy liczyć pochodną czy co.
a w pierwszym w ogóle topornie. Muszę to jutro oddać.
Jakby ktoś opisał krok po kroku na tym przykładzie było by super.
Dziękuje za pomoc. ;>
27 sty 09:48
Artur z miasta Neptuna:
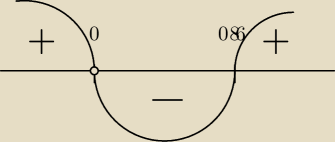
1.
D= R/{0}
f' = 0 ⇔ 3x
5+ x
4−2 = 0 ∨ x=0
tutaj miejsce zerowe wynosi ≈ 0.86 ∨ 0
f↗ w (−
∞, 0) i w (0.86;
∞)
f↘ w (0; 0.86)
27 sty 12:40
Artur z miasta Neptuna:
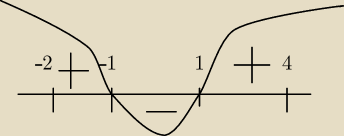
2.
D
f = R
f' = 3x
2 − 3
f' = 0 ⇔ x
2 − 1 = 0 ⇔ x=−1 ∨ x=1
ze szkicu wykresu pochodnej wiesz, że w x = −1 istnieje maksimum lokalne (ale niekoniecznie
globalne) oraz w x=1 istnieje minimum lokalne (ale niekoniecznie globalne).
Dlatego wyliczasz:
f(−2) = −8 + 6 = −2
f(−1) = −1 + 3 = 2
f(1) = 1 − 3 = −2
f(4) = 64 − 12 = 52
najmniejsza wartość to −2
największa to 52
w przedziale x∊<−2;4>
27 sty 12:48
GoodYou : dzięki. Ale w tym pierwszym chyba nie ma tego wszystkiego czego wymaga nasz wykladowca na
notatkach takie zadanie zajmuje 2 strony. hmmm
Mam coś takiego z wikipedii.
Własności wynikające wprost ze wzoru funkcji:
Dziedzina funkcji i punkty nieciągłości
Punkty przecięcia z osiami:
z osią 0X – miejsca zerowe
z osią 0Y – wartość w zerze.
Własności szczególne, takie jak parzystość, nieparzystość, okresowość, ciągłość itp.
Granice na końcach przedziałów określoności
Asymptoty
Własności wynikające z pierwszej pochodnej
Obliczenie pochodnej i wyznaczenie jej dziedziny
Przedziały monotoniczności
Ekstrema lokalne funkcji
Własności wynikające z drugiej pochodnej
Obliczenie drugiej pochodnej i wyznaczenie jej dziedziny
Przedziały wypukłości i wklęsłości
Punkty przegięcia
Zestawienie przebiegu zmienności funkcji w postaci tabelki na podstawie wiadomości uzyskanych z
punktów 1−4 i określenie zbioru wartości funkcji
Szkic wykresu funkcji
27 sty 13:06
GoodYou : dzięki. Ale w tym pierwszym chyba nie ma tego wszystkiego czego wymaga nasz wykladowca na
notatkach takie zadanie zajmuje 2 strony. hmmm
Mam coś takiego z wikipedii.
Własności wynikające wprost ze wzoru funkcji:
Dziedzina funkcji i punkty nieciągłości
Punkty przecięcia z osiami:
z osią 0X – miejsca zerowe
z osią 0Y – wartość w zerze.
Własności szczególne, takie jak parzystość, nieparzystość, okresowość, ciągłość itp.
Granice na końcach przedziałów określoności
Asymptoty
Własności wynikające z pierwszej pochodnej
Obliczenie pochodnej i wyznaczenie jej dziedziny
Przedziały monotoniczności
Ekstrema lokalne funkcji
Własności wynikające z drugiej pochodnej
Obliczenie drugiej pochodnej i wyznaczenie jej dziedziny
Przedziały wypukłości i wklęsłości
Punkty przegięcia
Zestawienie przebiegu zmienności funkcji w postaci tabelki na podstawie wiadomości uzyskanych z
punktów 1−4 i określenie zbioru wartości funkcji
Szkic wykresu funkcji
27 sty 13:07
Artur z miasta Neptuna:
oki ... już wiem ... myslałem że TYLKO monotoniczność
więc daj mi chwilkę
27 sty 13:08
Artur z miasta Neptuna: chwila chwila
| | 1 | |
czy f(x) = x2 + x + |
| − 1 |
| | x2 | |
| | 1 | |
czy f(x) = x2 + x + |
| |
| | x2−1 | |

zapewne to pierwsze −−− jeżeli tak to proszę pamiętać o nawiasach (albo nauczyć się zapisów na
forum)
27 sty 13:12
Artur z miasta Neptuna:
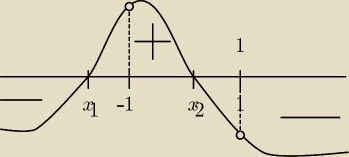
| | x2+x+1 | |
f(x) = |
| ; Df = R\{−1,1} |
| | x2−1 | |
| | x2−x+1 | |
f(−x) = |
| ≠ f (x) (f nie jest parzysta) |
| | x2−1 | |
| | −x2+x+1 | |
−f(−x) = |
| ≠ f(x) (f nie jest nieparzysta) |
| | x2−1 | |
asymptoty pionowe:
| | 3 | |
limx−>−1− f(x) = [ |
| ] = ∞ |
| | 0+ | |
| | 3 | |
limx−>−1+ f(x) = [ |
| ] = −∞ |
| | 0− | |
| | 1 | |
limx−>1− f(x) = [ |
| ] = −∞ |
| | 0− | |
| | 1 | |
limx−>1+ f(x) = [ |
| ] = ∞ |
| | 0+ | |
asymptoty poziome:
lim
x−>−∞ f(x) = 1
lim
x−>∞ f(x) = 1
Pochodna 1 rzędu:
| | (2x+1)(x2−1) − (x2+x+1)(2x) | | x2+4x+1 | |
f' = |
| = − |
| |
| | (x2−1)2 | | (x2−1)2 | |
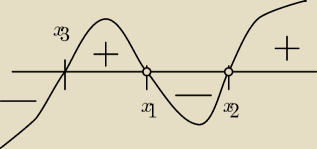
f' = 0 ⇔ x
2+4x+1 = 0 ⇔ x = −2 −
√3 (coś mniejszego od −1)∨ x = −2 +
√3 (coś wiekszego od
−1 a mniejszego od 1)
f↘ w (−
∞, x
1), w (x
2, 1) i w (1, +
∞)
f↗ w (x
1, −1), w (−1, x
2)
f posiada minimum lokalne w x
1 (wyznacz wartość f(x
1))
f posiada maksimum lokalne w x
2 (wyznacz wartość f(x
2))
27 sty 13:31
Waka:
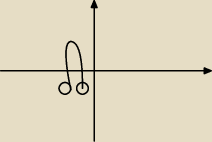
27 sty 13:41
Artur z miasta Neptuna:
pochodna 2 rzędu:
| | (2x+4)(x2−1)2−(x2+4x+1)2(x2−1)(2x) | |
f'' = − |
| = |
| | (x2−1)4 | |
| | x5+6x4+x3−4x2−3x−4 | |
= 2 |
| |
| | (x2−1)4 | |
D
f'' = D
f
f'' = 0 ⇔ x
5+6x
4+2x
3−4x
2−3x−2 = 0 ⇔ x = −1 ∨ x = 1 ∨ x = −2 −
3√3 −3
2/3 ≈ −5.5
punkt przegięcia TYLKO dla x
3 (x
1 = −1 i x
2=1 nie należą do D
f = D
f' = D
f'')
f wypukła gdy f''> 0 czyli f wypukła w (x
3, −1) i w (1,
∞)
f wklęsła gdy f''<0 czyli f wklęsła w (−
∞, x
3) i w (−1,1)
zapomniałem:
na początku jeszcze wyliczasz punkty przecięcia wykresu z osiami OX i OY
z OX:
| | x2+x+1 | |
0 = |
| ⇔ x2+x+1 = 0 sprzeczne bo ∀x∊Df x2+x+1 >0 |
| | x2−1 | |
z OY:
27 sty 13:53
Artur z miasta Neptuna:

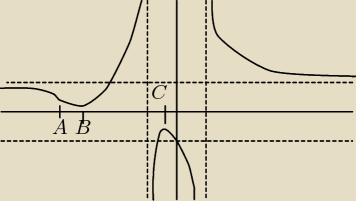
A −−− punkt przegięcia (wylicz wartość funkcji w tym punkcie)
B −−− minimum lokalne (wylicz wartość funkcji w tym punkcie)
C −−− maksimum lokalne (wylicz wartość funkcji w tym punkcie)
27 sty 13:59
Artur z miasta Neptuna:
27 sty 14:03
GoodYou : Wielkie dzięki.
Masz u mnie dużo piwo

=>
27 sty 16:48
 1.
D= R/{0}
1.
D= R/{0}
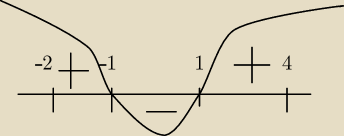 2.
Df = R
f' = 3x2 − 3
f' = 0 ⇔ x2 − 1 = 0 ⇔ x=−1 ∨ x=1
ze szkicu wykresu pochodnej wiesz, że w x = −1 istnieje maksimum lokalne (ale niekoniecznie
globalne) oraz w x=1 istnieje minimum lokalne (ale niekoniecznie globalne).
Dlatego wyliczasz:
f(−2) = −8 + 6 = −2
f(−1) = −1 + 3 = 2
f(1) = 1 − 3 = −2
f(4) = 64 − 12 = 52
najmniejsza wartość to −2
największa to 52
w przedziale x∊<−2;4>
2.
Df = R
f' = 3x2 − 3
f' = 0 ⇔ x2 − 1 = 0 ⇔ x=−1 ∨ x=1
ze szkicu wykresu pochodnej wiesz, że w x = −1 istnieje maksimum lokalne (ale niekoniecznie
globalne) oraz w x=1 istnieje minimum lokalne (ale niekoniecznie globalne).
Dlatego wyliczasz:
f(−2) = −8 + 6 = −2
f(−1) = −1 + 3 = 2
f(1) = 1 − 3 = −2
f(4) = 64 − 12 = 52
najmniejsza wartość to −2
największa to 52
w przedziale x∊<−2;4>
 zapewne to pierwsze −−− jeżeli tak to proszę pamiętać o nawiasach (albo nauczyć się zapisów na
forum)
zapewne to pierwsze −−− jeżeli tak to proszę pamiętać o nawiasach (albo nauczyć się zapisów na
forum)
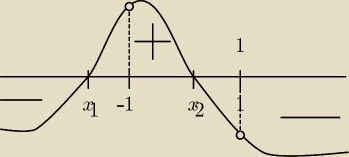

 pochodna 2 rzędu:
pochodna 2 rzędu:
 A −−− punkt przegięcia (wylicz wartość funkcji w tym punkcie)
B −−− minimum lokalne (wylicz wartość funkcji w tym punkcie)
C −−− maksimum lokalne (wylicz wartość funkcji w tym punkcie)
A −−− punkt przegięcia (wylicz wartość funkcji w tym punkcie)
B −−− minimum lokalne (wylicz wartość funkcji w tym punkcie)
C −−− maksimum lokalne (wylicz wartość funkcji w tym punkcie)

 =>
=>