PRzebieg zmiennosci funkcji
asia : muszę zbadać przebied monotoniczności funkcji f(x) = x3 + 6x2 + 9x
1. pierwsza pochodna f'(x) = 3x2 + 12x + 9
2. druga f'' = 6x + 12
3. punkty przecięcia z ox (−3,0) z oy (9,0)
4. ekstremum max f(−3) = −36 min f(−1) = −4
5. przedziały monotonicznosci, f. malejąca (−3, −1), f. rosnąca (− nieskonczonosc, −3> i <−1, +
niesk.)
6. z drugiej pochodnej x= −2
jak z tego policzyc te pkt, przegięcia i wypukłosc i wklęsłosc? punkt przeg, to f(x) = 0, wkl
f(x) > 0, a wyp. f(x) <0, jak to po podstawiac i wyliczyc? do 2giej pochodnej?
przy okazji, jak mozecie to sprawdzcie czy nie zrobiłam gdzies błędu ;c
26 sty 22:01
Aga1:
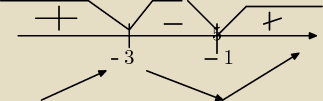
3. f(x) przecina oś ox w (0,0) i (−3,0), a oś oy w (0,0)
a f' ox (−3,0), (−1,0) a y w (0,9)
. miejsca zerowe pochodnej x
1=−3 i x
2=−1
f
max=f(−3)=(−27)+54−27=0
Do 5włącznie sprawdziłam.
26 sty 22:17
Aga1:

26 sty 22:50
asia: dzięki

27 sty 16:06
Aga1: "Piękny rysunek " z 22:50 to nie mój, ja nie mam takich zdolności plastycznych.
27 sty 16:08
 3. f(x) przecina oś ox w (0,0) i (−3,0), a oś oy w (0,0)
a f' ox (−3,0), (−1,0) a y w (0,9)
. miejsca zerowe pochodnej x1=−3 i x2=−1
fmax=f(−3)=(−27)+54−27=0
Do 5włącznie sprawdziłam.
3. f(x) przecina oś ox w (0,0) i (−3,0), a oś oy w (0,0)
a f' ox (−3,0), (−1,0) a y w (0,9)
. miejsca zerowe pochodnej x1=−3 i x2=−1
fmax=f(−3)=(−27)+54−27=0
Do 5włącznie sprawdziłam.

