. elpe: Wysokość trójkąta prostokątnego poprowadzona z wierzchołka kata prostego dzieli przeciwprostokatną na odcinki o dlugosciach p i q wykaż ze h=√p*q

rumpek: skorzystaj z podobieństwa trójkątów odpowiednie proporcje i wyjdzie

elpe: no wyszło dzięki rumpek

rumpek: ale chyba zrobię te zadanie dla przyszłych pokoleń

wolf:

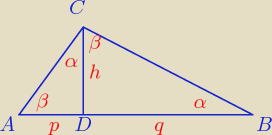rumpek: Z takim rysunkiem powinno być znacznie łatwiej oraz wygodniej Rozpatrzymy kąt |∡C| = 90^o, |∡A| = β, |∡B| = α. Rozpatrując trójkąt △BDC na podstawie sumy kątów w trójkącie widzimy, że: 180^o − 90^o − α = |∡BCD|. I teraz widzimy, że |∡C| = 90^o i otrzymujemy |∡ACD| = 90^o − |∡BCD| ⇔ |∡ACD| = α. Skoro wiemy już taką informację to również pozostało tylko zauważyć, że w całym trójkącie prostokątnym △ABC suma kątów wynosi 180^o, czyli: 180^o = 90^o + α + β ⇒ 90^o = α + β. Czyli z tego zauważamy, że dokładnie |∡BCD| to kąt β Trochę przydługi wstęp, ale specjalnie taki napisałem bo niektórzy nie widzą tych zależności. Teraz pozostało z podobieństwa trójkątów ułożyć odpowiednie proporcje dla trójkątów podobnych: △ADC ~△BDC (k,k,k).

h		q
	=
p		h

h² = p*q, h > 0 h = √pq c.n.u.

magda: Rumpek zorbiłeś dla przyszłych pokoleń bo i ja z tego skorzystałam dzięki