Ekstrema i monotonicznosc funkcji
Justyna: Ekstrema i monotonicznosc funkcji:
f(x)= 1/x
2 +8x ?
Wyliczam pochodna, korzystajac z wzoru na roznice szescianow zapisuje pochodna w postaci
iloczynu. W tym miejscu przyrownuje pochodna do zera i... wychodzi mi jedno miejsce zerowe.
Czy to znaczy, ze caly wykres bedzie nad osia X (nie liczac pkt x=1/2), co jest rownoznaczne,
ze minimum i maxim lokalne nie istnieja?

Prosze o pomoc!
26 sty 13:08
Aga: | | 1 | |
Czy o taką funkcję chodzi1)f(x)= |
| ? |
| | x2+8x | |
26 sty 13:12
Justyna: Aga, to wersja nr 2
26 sty 13:16
26 sty 13:27
Aga: f
'(x)=0
| | 3√2 | | 1 | |
x= |
| tak Ci wyszło? (a skąd x= |
| ?) |
| | 2 | | 2 | |
26 sty 13:31
Justyna: Kurcze, przepraszam bardzo! Zle spojrzalam na tresc zadania i przepisalam ( w dodatku z
bledem!) zamiast wzory funkcji, wzor pochodnej.
Od poczatku:
ekstrema i monotonicznosc dla:
f(x)= 1/x + 4 x2
wowczas: f'(x)=(−1)/(x)2 +8x
i z tego, przyrownujac do zera mam:
(2x−1)(4 x2 + 2x + 1)= 0
z pierwszego nawiasu x0=1/2, z drugiego −brak
26 sty 13:38
Aga1:
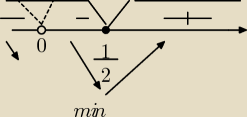
26 sty 13:45
Justyna: A dlaczego po lewej stronie od x=1/2 wystepuje minus?
Myslalam, ze zarowno z tej jak i prawej strony beda plusy
26 sty 14:48
Aga1: Możesz zawsze podstawić sobie liczbę z wybranego przedziału, a lepiej narysować wykres lub
tzw."węża"
26 sty 14:52
 Prosze o pomoc!
Prosze o pomoc!
