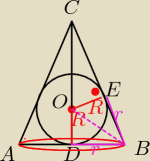
 H= ICDI=4R
W trójkącie COE IOCI=3R, IOEI=R
Z tw. Pitagorasa ICEI2=IOCI2−IOEI2
ICEI=2√2R
Znowu z twierdzenia Pitagorasa w trójkącie BCD
mamy (ICEI+r)2=r2+H2
Po podstawieniu i obliczeniu r=√2R
l=IBCI=3√2R
Podstaw do wzorów i porównaj.
H= ICDI=4R
W trójkącie COE IOCI=3R, IOEI=R
Z tw. Pitagorasa ICEI2=IOCI2−IOEI2
ICEI=2√2R
Znowu z twierdzenia Pitagorasa w trójkącie BCD
mamy (ICEI+r)2=r2+H2
Po podstawieniu i obliczeniu r=√2R
l=IBCI=3√2R
Podstaw do wzorów i porównaj.
 Pkuli = 4π*r2=4π*(√2R)2=4π*2R2=8πR2
Pstożka = πr(r+l)=π*√2R*(√2R+3√2R)=π*√2R*(4√2R)=8πR2
no a pole powierzchni całkowitej stożka ma być dwa razy większe od pola powierzchni kuli
Pkuli = 4π*r2=4π*(√2R)2=4π*2R2=8πR2
Pstożka = πr(r+l)=π*√2R*(√2R+3√2R)=π*√2R*(4√2R)=8πR2
no a pole powierzchni całkowitej stożka ma być dwa razy większe od pola powierzchni kuli
| 4 | 4 | 4 | ||||
Vkuli = | π*r3= | π*(√2R)3= | π*2√2R3= | |||
| 3 | 3 | 3 |
| 8√2*π*R3 | |
| 3 |
| 1 | 1 | |||
Vstożka = | π*r2*h= | π*(√2R)2 * 4R = | ||
| 3 | 3 |
| 1 | 1 | π* 8R3 | ||||
= | *π* 2R2 * 4R= | π* 8R3 = | ||||
| 3 | 3 | 3 |

| 4 | ||
2) Vk= | πR3 | |
| 3 |