BASIEK GDZIE JESTEŚ:) DZIADZIA: BASIEK GDZIE JESTEŚ

Basiek: Tu? O.o

DZIADZIA: jesteś jak miło od razu jestem już uśmiechnięty

Basiek: Właśnie doczołgałam się ze szkoły, dosłownie

DZIADZIA: Dzień dobry,jak mija dzionek?ja wczoraj już padłem,a Ty do której walczyłaś?

Basiek: 2:30 ? Coś koło tego. Dzionek okropny Ale będzie lepiej Z jakimi zadankami chcesz dziś powalczyć?

DZIADZIA: jesteś już na obrotach,czy dziś Twoje serduszko też jest takie dobre jak wczoraj i skłonne pomagać dziadzi?

DZIADZIA: ciągle ciągi mała

Basiek: Świetnie, ciągi to coś nad czym nie trzeba za wiele rozmyślać Może zacznijmy? Bo pewnie "trochę" zejdzie

DZIADZIA: dla jakiej wart x liczby 2, x+1, x+4 w podanej kol. tworzą ciąg geomet

DZIADZIA: wczoraj mi podawałas ^a1+a3₂=a2?

Basiek: Dla WSZYSTKICH zadań tego typu. Własność ciągu geometrycznego (a₂)²= a₁ * a₃ alternatywna forma a₂= √a₁*a₃ , polecam jednak pierwszą formę, to jak?

Basiek: Tak jest to jest własność ciagu arytmetycznego to z wczoraj: w ciągu geometrycznym wyraz środkowy to srednia arymetyczna w geometrycznym wyraz środkowy to średnia geometryczna Nawet dość logiczne.

DZIADZIA: a poza tym jak mam tu mam odswiezać korespondecie czy za kazdym razem muszę wychodzic?

Basiek: odświeżaj stronę?

krystek: Dzieciaki− jesli tak wolno!

	a1+a3
Ciąg arytmetyczny ⇒ stała różnica:a3−a2=a2−a1⇒a2=
	2

	a3		a2
Ciąg geom ⇒stały iloraz:		=		⇒(a2)2=a1*a3
	a2		a1

Basiek: Cześć Krystek ładnie ujęte.

krystek: Basiek metodycznie. Pozdrawiam !

DZIADZIA: (x+1)²=2*(x+4) x²+2x+1=2(x+4) ?

Basiek: Wymnóż, wszystko na jedną stronę... delta, pierwiastki ...

Basiek: Krystek a nie chciałoby Ci się czasem metodycznie wrzucić mi łopatą do głowy trygonometrii?

krystek: a o co chodzi?

Basiek: Prześladuje mnie jedna rzecz w równaniach trygonometrycznych, a zostałam uświadomiona, że za mniej niż 100 dni piszę maturę. Chodzi mi o wytłumaczenie ŁOPATOLOGICZNE (do mnie się chyba inaczej nie da...) , rozpisywanie serii rozwiązań dla sinusa i cosinusa. Niby niewiele..., ale za nic pojąć tego nie mogę

DZIADZIA: Δ=0 ^−b_2a=−1 i dalej nie wiem

krystek: Podaj .

Basiek: x²+2x+1=2x+8 x²=7 A może tak? Co teraz?

Basiek: No nie wiem, ja już jestem po sprawdzianie z tego kilka dobrych miesięcy ale np.

	1
a)sina=
	2

	1
b) sinβ= −
	2

Basiek: Moja wina, kazałam Ci się wpakować w deltę, bo nie patrzyłam na liczby i nie miałam pojęcia, że 2x się skrócą

DZIADZIA: dziele √ i wychodzi m√7 lub −√7 i jest to odp C

krystek: ok Po pierwsze wzory redukcyjne i znaki funkcji w poszczególnych ćwiartkach i dasz radę Możemy umówić sie na godz 19−ta ? Wszystko łopatolog wyjaśnie i zobaczysz jakie to łatwe

	1
sinx=
	2

jest dodatni w I i II ćwiartce czyli sinx=sin30 lub sinx=sin(180−30) x=30+k*360 lub x=150 +k*360

Basiek: No, super Wrzuć następne

Basiek: 19−ta? Będę ! Kurczę, pierwszy raz widzę to rozpisane za pomocą wzorów redukcyjnych... ale wygląda dużo przyjemniej To do potem

Święty: Matura z matmy za 103 dni

DZIADZIA: Basiu a pamiętasz to wczorajsze zadanie ile ujemnych wyrazow ma ciąg bla bla bla an=2n²−25n+72 no i wyliczyłem (4¹₄,8) ale nie wiem jak mam wiedzieć ile jest tych wyr wyr ujemnych?

Basiek: Święty buuu, nie strasz dzieci! Dziadzia Kluczem jest uświadomienie sobie czym jest n we wzorze, bo na koniec wyliczyłeś,

	1
ze n∊(4		,8) n to jest liczba porządkowa, numer jakiegoś wyrazu ciągu...
	4

a_n czyli np. n=1 a₁ , n=5 a₅ i n zawsze w ciągach jest liczbą naturalną >0 wyobrażasz sobie wyraz ciągu a_1/1234 ? więc ile takich wyrazów ciągu z takiego przedziału może być?

	1
a4		rzecz jasna odpada, zresztą, nawet niedomknięty przedział..., ale a5, a6, a7
	4

(a₈ też niedomknięty) łącznie 3 takie wyrazy, tak?

DZIADZIA: jesteś super kurde musze zdobyć te zakichane minimum 15pkt funkcje mam opanowane z tego zawsze jest jakies 5pkt w zamknietych prawda na czym mam się skupić Twoim zdaniem jeśli zalezy mi na 15pkt

kylo1303: Ja to bym sie skupil na nauce myslenia, reszta juz pojdzie z gorki xD

krystek:

	√2
cosx=−		}
	2

cosx=−cos45 i cos ujemny w II i III ćwiartce cosx= cos(180−45) lub cosx=cos(180=45) i teraz dokończysz? pisze w stopnowej mierze dla ułatwienia zapisu! Pomogło?

krystek:

	√2
cosx=−		}
	2

cosx=−cos45 i cos ujemny w II i III ćwiartce cosx= cos(180−45) lub cosx=cos(180+45) i teraz dokończysz? pisze w stopnowej mierze dla ułatwienia zapisu! Pomogło?

Basiek: Kylo jak zawsze milusi Dziadzia gdyby był jakikolwiek wzór, który by to regulował, to wszyscy by zdawali... , ale jeśli coś jest i pojawia się regularnie to : wielomian, procenty, kąty w pole, trójkąt 30,60,90. Łap: od str 35. http://www.cke.edu.pl/images/stories/Inf_mat_od2008/matematyka_a.pdf

DZIADZIA: an=23−⁴₇n ktorym wyrazem ciagu jest liczba 3? A35 B42 C49 Dżaden wyraz nie jest równy 3

Tragos: 23 − U{4}[7}n = 3 U{4}[7}n = 20 4n = 140 n = 35 ODP. A

krystek:

	1
sinx=−
	2

sinx=−sin30 i teraz wzory redukcyjne sin ujemny w III i IV ćwiartce sinx=sin(180+30) lub sinx=sin(360−30) x=210+k*360 lub sinx=330+k*360

Basiek: Trochę lepiej Krystek

	3π		5π
x=		+ 2kπ v x=		+2kπ
	4		4

Jeśli dobrze łapię, to coś teraz, to ja bym tam raczej wpisała: cosx=cos(270−45), że niby 270 od 3ćw i minus 45.

Basiek: Widzisz, w tym drugim przykładzie, to już niestety... nie bardzo. dlaczego w tej pierwszej serii nie może być sinx=sin(270−30) ?

krystek: Przy nieparzystej wielokrotności kąta 90 cos zamienia sie na sin a sin na cos! I tak cos (270−45)=−sin45 i tu sie zgadza bo sin i cos 45( i w III ćwiartce obydwie funkcje są ujemne!) jest taki sam. Ale weź sin(270−30)=?

kylo1303: Taka wskazowka: przy 90 i 270 funkcje sie zmieniaja (sinus przechodzi w cosinus). Tez wiec warto to zapamietac: Os pionowa− przechodzi w inna Os pozioma− nie przechodzi.

krystek: Przy nieparzystej wielokrotności kąta 90 cos zamienia sie na sin a sin na cos! I tak cos (270−45)=−sin45 i tu sie zgadza bo sin i cos 45( i w III ćwiartce obydwie funkcje są ujemne!) jest taki sam. Ale weź sin(270−30)=?

krystek: Do 19−te! wszystko spokojnie wyjaśnię w układzie współrzędnych , dla dowolnego kąta. papa

Basiek: Ożesz. Faktycznie! Ja tu wiecie, w ogóle abstrahowałam od pojęć takich jak kofunkcje itd., a fakt faktem tu to się łączy... wszystko zaczyna się sklejać w mały, pogruchotany wazonik, ale już lepiej. kylo− o jakich osiach mówisz? Bo tego jednego nie rozumiem

kylo1303: Sory, skrot myslowy. Przy wyprowadzaniu funkcji operowalismy na ukladzie wspolrzednych. Pierwsza cwiartka to katy 0−90, druga 90−180 itd. Czyli Os OY wyznacza jakby kat 90 (powyzej osi OX) oraz 270 (ponizej OX). Os OX wyznacza kat 0/360 i 180.

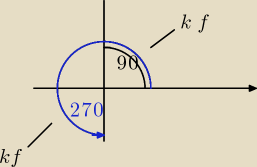
Tragos: kf. − kofunkcja

Basiek: Wiedziałam o co chodzi w kofunkcji. Przynajmniej tak myślałam. Wiem już, że się myliłam. Dzięki.

Basiek: Dziadzia nie śpimy Cóż Ty tak namiętnie teraz liczysz?

DZIADZIA: w ciag geom o ilorazi q=³₂ suma 4pierwszych wyrazow jest rowna 65 wobec tego a1=?

Basiek: S₄= 65

	3
q=
	2

n=4 wzór na sumę w ciągu geom?

DZIADZIA: Sn=a1*^1−qn_1−q

Basiek: No? I w czym problem? Podstawiasz i wyliczasz a₁

Basiek:

	3   1−( )4   2
65=a1
	3   1−   4

DZIADZIA: a ja zrobiłem do kwadratu imi wyszło a1=60

Basiek: To jeszcze raz Do skutku. A ja po kawę

DZIADZIA: mianownik q ³₂ widze ze najlepszym sie byki zdarzają

Basiek: Właśnie... wiesz co? Ja jednak bez snu nie pociągnę. Będę za godzinkę, co? Dobranoc

DZIADZIA: pogubiłem się tu bla bla tre tre =a1* (−⁶⁵₈*(−²₁)= =a1*⁶⁵₈

DZIADZIA: nie wiem jak dam sobie rade bez Ciebie ale spróbuję a ja też około 19 wyskocze na 1,5h na trening

Basiek:

	81   1−   16
65= a1 *
	1   −   2

	16   81   − 16   16		1
65=a1*		/ * −
	1   −   2		2

	65		−65
−		= a1 *
	2		16

Teraz sobie poradzisz Jeszcze raz dobranoc