liczby zespolone Bartek: Korzystając z interpretacji geometrycznej modułu różnicy liczb zespolonych narysować zbiory liczb zespolonych spełniających podany warunek: |z + i| + |z − i|=2 Ja to zrobiłem o tak. W miejsce z oraz i wstawiłem √x² + y² + √0² + 1² i tak dalej. Na koniec wyszło mi coś takiego: x² + y²=1 i nie wiem czy dobrze,bo im wyszło o takie coś: na rysunku na górze ma być i a na dole według nich jest −i. Nic nie rozumiem.

Bartek: w treści powinno być: narysować zbiór liczb zespolonych spełniających... Po prostu z zadaniu jest więcej przykładów.

Bartek: A swoją drogą, szkoda, że nie wiem jak się piszę tutaj w rysowaniu litery i liczby,bo to by znacznie ułatwiło i upiększyło rysunek.

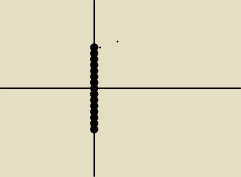
pigor: tu nic nie musisz liczyć tylko zauważyć, że tę równość sumy modułów {z+i| +{z−i}=2 obrazuje geometrycznie zbiór liczb z , których suma odległości od liczb 0−1i oraz 0+1i , czyli od "punktów" (par) (0,−1) i (0,1) jest równa 2 , a więc dokładnie i obrazowo właśnie ten czarny "łańcuszek" liczb z (odcinek liczb z) na osi urojonej Iz

pigor: a więc "im" dobrze wyszło jak na tym rysunku

Bartek: czyli tu chodzi o to, że jest powiedzmy z=x+iy , ale x=0 oraz y=1 więc mam z=0 +1i czyli z − 1i a w przypadku z=0 − 1i mam z + 1i . Nie no, chyba coś pomieszałem...oj ciężko u mnie z tym ciężko