gloov: hmm jeśli |BD|=|DC| to znaczy, że to Δ równoramienny, czli kąty w ΔBCD przy wierzchołkach B i C
są takie same. Wtedy |AB|=|BC|, czyli ΔABC jest równoramienny i kąty przy wierzchołkach A i C
musza być takie same. Czyli wychodzi na to, że jeżeli kąty DBC i DCB są takie same to taki sam
jest też kąt BAC.
Tylko jak to wykazać
?
Może ktoś pomóc?
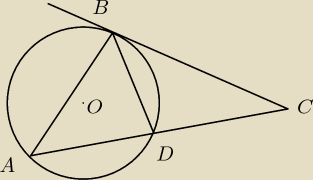Wykaż, że jeśli |BD|=|DC|, to |AB|=|BC|. Półprosta CB jest styczna do okręgu w pkcie B.