Ostrosłup Ewa: W ostrosłupie prawidłowym czworokątnym o podstawie ABCD i wierzchołku S dane są: |AB|= a i |AS|= 2a. Wyznacz: a) objętość i pole powierzchni całkowitej tego ostrosłupa.

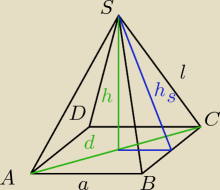
dero2005: l = 2a d = a√2

	√14
h = √l2 − (d2)2 = √(2a)2 − (a√22)2 = a
	2

	a2*h		a3√14
V =		=
	3		6

h_s = √h² + (^a₂)² = −−−−−− P_b = 2*a*h_s = −−−−−−− P_p = a² P_c = P_p + P_b = −−−−−−−−

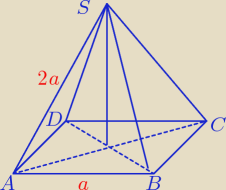rumpek: Pomagam, wpierw rysunek

rumpek: Widze, że jeszcze odpowiedzi nie ma także dokończe

rumpek: Spodek wysokości (punkt przecięcia się wysokości podstawy) określmy O. Wiemy, że podstawa tego ostrosłupa to kwadrat, zatem: pole podstawy będzie to: P_p = a * a = a² [j²] Pozostało obliczyć wysokość |SO| ostrosłupa. Korzystamy z tw. Pitagorasa w trójkącie ASO, i otrzymujemy: |AO|² + H² = |AS|²

	a√2
(		)2 + H2 = 4a2 (odcinek |AO| to dokładnie połowa przekątnej kwadratu a√2)
	2

2a2
	+ H2 = 4a2
4

	2a2
H2 = 4a2 −
	4

	16a2 − 2a2
H2 =
	4

	14a2
H2 =		, H > 0
	4

	√14a
H =
	2

	1
V =		*Pp * H
	3

	1		√14a
V =		* a2 *
	3		2

	a3√14
V =		[j3]
	6

2. Liczę pole powierzchni całkowitej ostrosłupa: P_c = P_p + P_b

	1
Pb = 4 *		* a * h
	2

Pozostało obliczyć niewiadomą h, również z trójkąta prostokątnego. dla ASG (G to połowa odcinka |AB|), zatem liczymy: |GS|² + |AG|² = |AS|²

	a2
h2 +		= 4a2
	4

	a2
h2 = 4a2 −
	4

	16a2 − a2
h2 =
	4

	15a2
h2 =		, h > 0
	4

	√15a
h =
	2

Podstawiamy pod wzór i mamy:

	1		a√15
Pb =		* 4 * a *
	2		2

	a2√15
Pb = 2 *
	2

P_b = a²√15 P_c = a² + a²√15 P_c = a²(1 + √15) [j²]

Ewa: Wielkie dzięki