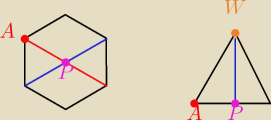
 a)
1) Wyznaczasz długość krawędzi bocznej
2) Wyliczasz połowę przekątnej podstawy (czyli AP)
3) Z sinusa lub tangensa obliczasz wysokość ostrosłupa
4) Obliczasz objętość
a)
1) Wyznaczasz długość krawędzi bocznej
2) Wyliczasz połowę przekątnej podstawy (czyli AP)
3) Z sinusa lub tangensa obliczasz wysokość ostrosłupa
4) Obliczasz objętość
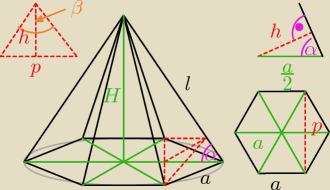 l = 3a
H = √l2 − a2 = √(3a)2 − a2 = √9a2−a2 = √8a2 = a√8 = 2a√2
l = 3a
H = √l2 − a2 = √(3a)2 − a2 = √9a2−a2 = √8a2 = a√8 = 2a√2
| 3a2√3 | ||
Pp = | ||
| 2 |
| Pp*H |
| |||||||||
V = | = | = a3√6
| ||||||||
| 3 | 3 |
| H | 2a√2 | h | ||||
sinα = | = | = | ||||
| l | 3a | a2 |
| a√3 | ||
h = | ||
| 3 |
| p2 |
| 3 | ||||||||||
tgβ2 = | = | = | ||||||||||
| h |
| 2 |
 Witam. w związku, że zadanie nie zostało do końca poprawnie rozwiązane a również mam z nim
problem chciałbym odświeżyć temat.
Otóz tgβ (nie zmieniajmy oznaczeń) liczę następująco:
Witam. w związku, że zadanie nie zostało do końca poprawnie rozwiązane a również mam z nim
problem chciałbym odświeżyć temat.
Otóz tgβ (nie zmieniajmy oznaczeń) liczę następująco:
| a √35 | ||
Wyliczam h ściany bocznej z TW Pitagorasa→wychodzi mi | ||
| 2 |
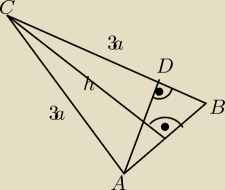
| AD | h | ||
= | h to wysokość ściany bocznej, CB to krawędź ostrosłupa a więc wynosi | ||
| a | 3a |
| h | a √35 | |||
AD= | = | |||
| 3 | 6 |
| a √35 | a √35 | a √35 | ||||
(a √3)2=( | )2 + ( | )2 − ( | )2 cosβ | |||
| 6 | 6 | 6 |
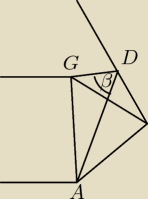 Odcinek AG − 2 wysokości w trójkącie równobocznym
Odcinek AG − 2 wysokości w trójkącie równobocznym
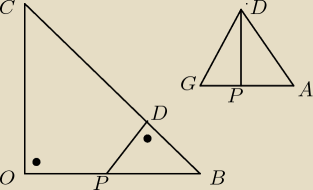 O − spodek wysokosci ostroslupa
P − punkt przecięcia prostych OB i GA (przecinaja się pod kątem prostych ponieważ figura ABGO
jest rombem, reszta wedlug oznaczen Krl. zalączam też rysunek pomocniczy
α − kat GDA
tgα=?
β=α/2 (Beta jest to kąt ADP − albo jak kto woli AGD)
|GA| = 2(a√3)/2 −> |PA| = a√3/2
tgβ= |PA| / |DP|
Δ COB ~ Δ DPB (cecha KK oba są prostokątne i maja wspolny kat B)
|DB| = |OB| * |PB||CB| = a6
z tw pitagorasa liczę |PD| i mam |PD|=2√2a6
tgβ=|PA||PD|=3√64
korzystam ze wzoru na tangens podwojonego kąta tg2α=2tgα1−tg2α , tylko że za 2α=β
rachuję i mam: tgα=−12√619
O − spodek wysokosci ostroslupa
P − punkt przecięcia prostych OB i GA (przecinaja się pod kątem prostych ponieważ figura ABGO
jest rombem, reszta wedlug oznaczen Krl. zalączam też rysunek pomocniczy
α − kat GDA
tgα=?
β=α/2 (Beta jest to kąt ADP − albo jak kto woli AGD)
|GA| = 2(a√3)/2 −> |PA| = a√3/2
tgβ= |PA| / |DP|
Δ COB ~ Δ DPB (cecha KK oba są prostokątne i maja wspolny kat B)
|DB| = |OB| * |PB||CB| = a6
z tw pitagorasa liczę |PD| i mam |PD|=2√2a6
tgβ=|PA||PD|=3√64
korzystam ze wzoru na tangens podwojonego kąta tg2α=2tgα1−tg2α , tylko że za 2α=β
rachuję i mam: tgα=−12√619