liczby zespolone
Bartek: Wie ktoś jak to rozgryźć?Korzystając z interpretacji geometrycznej modułu różnicy liczb
zespolonych narysować zbiory liczb zespolonych spełniających podany warunek:
|2iz + 6|≤4
Wiem, że i=(0,1) oraz że |z|=√x2 + y2, ale dalej nie wiem...co mam zrobić z 2iz ?
Jeśli chodzi o całość, pomyślałem sobie, że można z tego zrobić takie coś: |2iz −(− 6)|≤4
Ale dalej nie wiem.
22 sty 17:57
pigor:
|2iz+6|≤4 i niech z=x+iy , to 2|i(x+iy)+3|≤4 /:2 , czyli
|ix−y+3|≤2 /2 obustronnie
|3−y+ix|2≤4 , czyli (3−y)2+x2≤ 4 , a więc
x2+(y−3)2≤ 22 , a to jest zbiór punktów z=(x,y)
koła o środku w (0,3) i promieniu r=
22 sty 18:11
Bartek: Nie rozumiem tego, co jest po lewej od "obustronnie". Czemu napisałeś |ix−y+3|≤2 ?
Przecież jest : |ix +i
2y +3|

Czemu tam jest znak "−" i czemu jest zjedzone i
2 ?
22 sty 18:24
Bartek: Okej, już mam. Przecież i
2=(−1,0) czyli −1.
Analizuję dalej

22 sty 18:28
pigor: bo | i*(x+iy)+3 | = | ix+i2y+3 | = | ix−y+3 | , bo i2=−1
22 sty 18:28
Sławek:
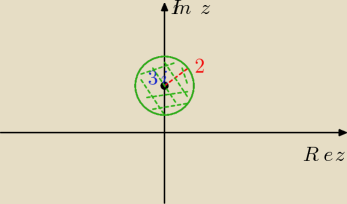
Doprowadzasz wyrażenie do postaci: |z − z
0| ≤ r
z
0 to współrzędne środka koła o promieniu r
Wykorzystaj też poniższą własność modułu liczby zespolonej:
|z
1 * z
2| = |z
1| * | z
2|
|2iz + 6| ≤ 4
|2i| |(z − 3i)| ≤ 4
2 |z − 3i| ≤ 4
|z − 3i| ≤ 2
22 sty 18:31
Bartek: Okej, to doszedłem już do tego: |ix +(3−y)|2≤4 czyli (3−y)2+x2≤ 4 Jeżeli jednak
i2=−1, to dlaczego po zniesieniu modułu jest "+x2" ? Załapałem, że właśnie z powodu
opuszczenia modułu, ale nie jestem pewny...
22 sty 18:36
Sławek:
Wydaje mi się, że w zestawieniu z treścią zadania zaproponowane przeze mnie rozwiązanie jest
lepsze.
Cytat: Korzystając z interpretacji geometrycznej modułu różnicy liczb zespolonych
narysować zbiory liczb zespolonych spełniających podany warunek:
22 sty 18:40
Bartek: Rany julek, jakie to się proste wydaje teraz. Nie rozumiem jednak jednego. Przecież i to jest
(0,1). Więc 2i=(0,2) Dlaczego więc po opuszczeniu modułu |2i| jest 2 ? Myślałem, że 2*(1,0)=2
a nie 2*(0,1) .
Zatem czy liczbę 2 można zapisać w postaci liczby zespolonej (0,2) czy (2,0)

Bo to jest
właśnie nieścisłość, które mnie męczy.
22 sty 18:45
Sławek:
Bo
z= x + iy
|z|= √x2+y2
czyli
z = 2i
|z|= √02 + 22 = √4 = 2
22 sty 18:49
Sławek:
Jeżeli zapisujesz liczbę zespoloną jako uporządkowana parę liczb rzeczywistych (x,y)
to w postaci algebraicznej (z=x+iy) liczby zespolonej 'x' oznacza część rzeczywistą a 'y' część
urojoną.
22 sty 18:55
Bartek: | | 3 | |
A czemu liczbę |
| zastąpiłeś liczbą −3i ? Czy liczba −3i=(0,−3) |
| | i | |
22 sty 18:55
Sławek:
Bo
| 3 | | 3*i | | 3*i | |
| = |
| = |
| = −3i |
| i | | i*i | | −1 | |
i
2 = −1
22 sty 18:59
Bartek: Rany, dzięki Sławek. Wiesz, teraz usiłuję rozgryźć inne, ale wychodzą mi jakieś głupoty.
Zacząłem o tak:
2<|z+2−i|≤3 więc mam
|(z +2) −i|>2
|(z +2) −i|≤3 teraz to do kwadratu
wychodzi mi jednak coś takiego i nie wiem czy jest ok:
|(z+2)2 −i2|>22 czyli mam (z+2+i)(z+2−i)>4 i co? działać dalej czy to pomysł do bani?
22 sty 19:16
Bartek: Oczywiście jeszcze moduł dochodzi, ale już zapomniałem o nim.
22 sty 19:17
Bartek: Czyli do bani

Okej, to myślę dalej.
22 sty 19:23
Sławek:
2 < |z+2−i| ≤3
2 < |z − (−2+i)| ≤3
22 sty 19:23
Bartek: kurcze, że ja zawsze widzę to, co widzi humanista a nie to,co widzi matematyk. Niech to..
Ale rozumiem, że najpierw robię:
|z − (−2+i)|>2
a potem
|z − (−2+i)| ≤3. No tak ..tylko, że nie wiem jednego. Czy działania na liczbach zespolonych w
postaci algebraicznej można łączyć z postacią (x,y). Bo nie wiem czy teraz ma wykonać
dodawanie (−2+i)=(−2,1)

22 sty 19:32
Sławek:
To będzie pierścień. Promień zewnętrznego koła R = 3, mniejszego (bez okręgu − bo nierówność
jest ostra) r = 2. Środek w punkcie z0 = −2 +i
22 sty 19:33
Bartek:
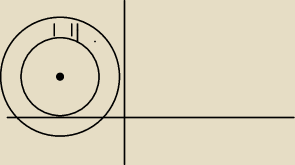
Rozumiem, że to ma być między kołami. Nie chwytam jednak jednego. Dlaczego ten nasz środek
(−2,1) jest początkiem promieni r oraz R skoro geometrycznie modułem liczby zespolonej z jest
odległość punktu z od początku układu współrzędnych?
22 sty 19:55
Bartek: Okej, okej, już chyba zrozumiałem.
22 sty 20:02
Bartek: Zrozumieć zrozumiałem i podobne przykłady już rozwiąże, ale mam jeszcze taki jeden nie
podobny.Gdyby chodziło tylko o licznik albo tylko o mianownik, to byłoby proste. Tu chodzi
jednak o iloraz, do którego mi już siło brakuje:
| | z−3 | | z | | 3 | |
| |
| |>1 i to zaczałem robić tak: | |
| − |
| |>1 teraz nie wiem.. |
| | z−3i | | z−3i | | z−3i | |
22 sty 20:19
Bartek: Sławek to już pewnie dał sobie ze mną spokój, ale może ktoś inny? Please...

22 sty 20:34
Sławek:
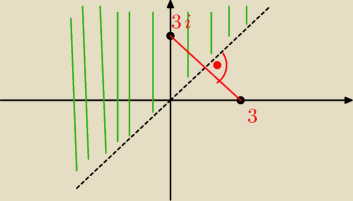
wykorzystujemy własność
i w twoim przykładzie dla z≠3i mamy
|z−3| > |z−3i|
rozwiązaniem jest półpłaszczyzna ograniczona symetralną odcinka o końcach z
1=3 i z
2=3i bez
punktu z
2=3i oraz bez symetralnej (bo nierówność jest ostra).
22 sty 21:50
Sławek:
na rysunku tam gdzie jest 3i ma być puste kółeczko
22 sty 22:22
 Czemu tam jest znak "−" i czemu jest zjedzone i2 ?
Czemu tam jest znak "−" i czemu jest zjedzone i2 ?

 Doprowadzasz wyrażenie do postaci: |z − z0| ≤ r
z0 to współrzędne środka koła o promieniu r
Wykorzystaj też poniższą własność modułu liczby zespolonej:
|z1 * z2| = |z1| * | z2|
|2iz + 6| ≤ 4
Doprowadzasz wyrażenie do postaci: |z − z0| ≤ r
z0 to współrzędne środka koła o promieniu r
Wykorzystaj też poniższą własność modułu liczby zespolonej:
|z1 * z2| = |z1| * | z2|
|2iz + 6| ≤ 4
 Bo to jest
właśnie nieścisłość, które mnie męczy.
Bo to jest
właśnie nieścisłość, które mnie męczy.
 Okej, to myślę dalej.
Okej, to myślę dalej.

 Rozumiem, że to ma być między kołami. Nie chwytam jednak jednego. Dlaczego ten nasz środek
(−2,1) jest początkiem promieni r oraz R skoro geometrycznie modułem liczby zespolonej z jest
odległość punktu z od początku układu współrzędnych?
Rozumiem, że to ma być między kołami. Nie chwytam jednak jednego. Dlaczego ten nasz środek
(−2,1) jest początkiem promieni r oraz R skoro geometrycznie modułem liczby zespolonej z jest
odległość punktu z od początku układu współrzędnych?

