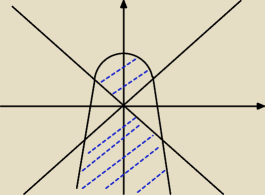
całka podwójna ***Całka***: Znajdź granice całkowania ∬f(x,y)dxdy D D= {f(x; y) : y²≥ x² ∧ y ≤4−x² } Sama próbowałam narysować sytuację, ale nie umiem określić zb. D. Proszę mi powiedzieć czy rys. jest dobry i jak dalej to opisać?

Krzysiek: jak widać z rysunku możesz podzielić obszar na 2 obszary (i te na 2 takie same ) więc niech D₁ oznacza obszar górny (prawy) łatwiej będzie określić grancie całkowania jeżeli będziemy całkować po y (po x będziemy musieli rozbić na 2 obszary) więc: obliczamy punkt przecięcia: y=x i y=4−x²

	1
wiec x=		(√17−1)
	2

czyli:

	1
0≤x≤		(√17−1)
	2

x≤y≤4−x²

Całka: górną potrafię, ale i tak dziękuję za odpowiedź. jak opisać dolną część? Problem właśnie tkwi w tej części, dla której y∊<0,−∞)?