Ekstrema DRLZ: Hej! Mógłby mi ktoś wytłumaczyć ogółem wzory jeżeli chodzi o ekstrema funkcji? Mianowicie wiem, że jest warunek konieczny: f(x)' = 0 Ale nie rozumiem warunków wystarczających.... Pomoże ktoś?

Aga: Na początek napisz jakiś prosty przykład a) funkcję wielomianową b) funkcję wymierną.

DRLZ: Hmm... f(x) = x³ − 9x + 6

	x3
f(x) =
	x2 − 3

DRLZ: Oraz przy okazji mam też problem z zadaniami ' znaleźć punkty przegięcia i wyznaczyć przedziały wklęsłości i wypukłości"

	x2 +1
mam np. zadanie: f(x)=
	x−2

Wiem, że należy obliczyć f'(x) i kolejno f '' (x) i f '' (x) = 0 Ale wynik f '' (x) = 10x−20 => x=2 ... I nie wiem czy bład w obliczeniach czy w myśleniu/rozumowaniu...

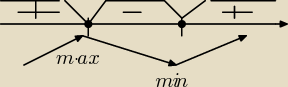
Aga: a) obliczasz pochodną f^'(x)=3x²−9 Rozwiązujesz równanie f^'(x)=0⇔3x²−9=0 x₁=−√3, x₂=√3 Są to punkty podejrzane o ekstremum. ( jeśli pochodna nie ma miejsc zerowych, to nie ma ekstremum) Rysujesz wykres, tu parabolę ,zaznaczasz, gdzie pochodna przyjmuje wartości dodatnie, a gdzie ujemne. Przy okazji wychodzą Ci przedziały monotoniczności, jak + to funkcja rosnąca, strzałka do góry, jak − to strzałka do dołu. Powstała niby górka i dołek. Na górce jest max y_max=f(−√3)=(−√3)³−9(−√3)+6=−3√3+9√3+6= W dołku min y_min=f(√3)= Przykład b) rozwiąż to Co później sprawdzę.

Aga: Na razie Ci więcej nie pomogę, bo inne obowiązki wzywają.

Aga: Czy jest to zrozumiałe?