Podziękowania Godzio: Trivial jestem Ci niezmiernie wdzięczy za pomoc, jak kiedyś byś wpadł na jakikolwiek pomysł w jaki mogę Ci się odwdzięczyć to pisz Wykładowca chodził, a ćwiczeniowiec siedział sobie przy biurku i widział jak nasz cały rząd ściąga, właściwie 3/4 ściągało, ale patrzył głównie na nas i się śmiał Ufff

Eta: A to takie "kwiatki" ? ...

rumpek: Godzio widzę, że masz dobry humor więc mógłbym poprosić o jakieś typowo maturalne zadania z "wykaż, że" dotyczące planimetrii ?

Kasia: http://img.naszemiasto.pl/grafika2/nowy/a1/ba/4f0daf85c507a_z.pdf

Kasia: zad 9 chociażby

Godzio: Hehe, czy to nie było ostatnio ?

rumpek: W sensie "nie było ostatnio"? Tak prosiłem o zadania z wykaż, że ale kazałeś odezwać się następnego dnia xD A niestety zapomniałem

Godzio: Chodziło mi o to zad. 9 Czekaj poszukam zaraz czegoś

Godzio: Zad. 1 Na okręgu o średnicy d opisano trapez równoramienny o podstawach a i b. Udowodnij, że d = √ab Zad. 2 Wykazać, że jeżeli w trójkącie środkowa jest 2 razy krótsza od boku do którego została poprowadzona, to trójkąt jest prostokątny. Zad. 3 Wykazać, że jeżeli α,β,γ są kątami trójkąta i zachodzi związek:

	sinα + sinβ
sinγ =		to trójkąt jest prostokątny
	cosα + cosβ

Zad. 4 Wykaż, że jeżeli zachodzi 1 + cos²(α + β) = cos²α + cos²β, gdzie α i β to kąty pewnego trójkąta, to ten trójkąt jest prostokątny Zad. 5 W kwadracie, którego bok ma długość 1 zawarty jest trójkąt. Udowodnić, że pole trójkąta nie jest większe niż sinus dowolnego jego kąta

rumpek: Ok, thx za zadanka jutro zrobię

rumpek: Zadanie 1 Z własności wpisania okrąg w czworokąt wiemy, że: a + b = c + d. Stosując to do trapezu

	a + b
równoramiennego mamy: 2c = a + b / : 2 ⇒ c =		. Średnica d to inaczej wysokość
	2

	a − b
trapezu równoramiennego. Wiem również, że x =		(a > b). Z twierdzenia Pitagorasa
	2

otrzymuję: d² + x² = c²

	(a − b)2		(a + b)2
d2 +		=		/ * 4
	4		4

4d² + (a − b)² = (a + b)² 4d² + a² − 2ab + b² = a² + 2ab + b² 4d² = a² − a² + 2ab + 2ab + b² − b² 4d² = 4ab / : 4 d² = ab, d∊R₊ d = √ab c.n.u.

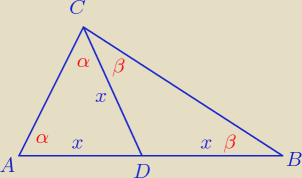
rumpek: Zadanie 2 Na podstawie rysunku możemy stwierdzić, że mamy do czynienia z dwoma trójkątami równoramiennymi. Widzimy, że podstawa |AB| = 2x, |CD| = x. Zatem kąty w trójkącie ADC przy podstawie są sobie równe. Podobnie z trójkącie CDB. To na podstawie tych informacji i zaznaczonych kątów, pozostało skorzystać tylko z sumy miar kątów wewnątrz trójkąta: α + β + α + β = 180^o 2α + 2β = 180^o / :2 α + β = 90^o (trójkąt ma kąt prosty zatem jest to trójkąt prostokątny) c.n.u.

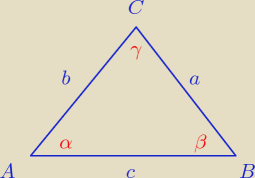
rumpek: Wpierw rysunek do zadania 3, które napisze jakoś tak za 30 − 40 minut

rumpek: Z tw. sinusów otrzymuje: 1^o

	c
2R =		/ * sinγ
	sinγ

c = 2Rsinγ / : 2R

	c
sinγ =
	2R

2^o

	a
2R =		/ * sinα
	sinα

2Rsinα = a / : 2R

	a
sinα =
	2R

3^o

	b
2R =		/ * sinβ
	sinβ

2Rsinβ = b / : 2R

	b
sinβ =
	2R

Tw. cosinusów: 1^o a² = b² + c² − 2bccosα −2bccosα = a² − b² − c² / (−2bc)

	a2 − b2 − c2
cosα =
	−2bc

2^o b² = a² + c² − 2accosβ −2accosβ = b² − a² − c² / : (−2ac)

	b2 − a2 − c2
cosβ =
	−2ac

	sinα + sinβ
Podstawiając pod tezę zadania: sinγ =
	cosα + cosβ

c		a   b   + 2R   2R
	=
2R		a2 − b2 − c2   b2 − a2 − c2   + −2bc   −2ac

c		a + b   2R
	=
2R		a3 − ab2 − ac2   b3 − ba2 − c2   + −2abc   −2abc

c		a + b		−2abc
	=		*		/ * 2R
2R		2R		a3 − ab2 − ac2 + b3 − ba2 − c2

	(a + b) * (−2abc)
c =
	a3 − ab2 − ac2 + b3 − ba2 − c2

	−(a + b)(2abc)
c =
	−a(b2 + c2 − a2) − b(a2 + c2 − b2)

	(a + b)(2abc)
c =		/ : c (a,b,c > 0)
	a(b2 + c2 − a2) + b(a2 + c2 − b2)

	(a + b)(2ab)
1 =		/ * mianownik
	a(b2 + c2 − a2) + b(a2 + c2 − b2)

(a + b)2ab = (−a³ − b³) + ba² + ab² + ac² + bc² (a + b)2ab =(ba² + ab²) + (ac² + bc²) − (a³ + b³) (a + b)2ab = ab(a + b) + c²(a + b) − (a + b)(a² − ab + b²) / : (a + b) 2ab = ab + c² − a² + ab − b² 2ab = c² + 2ab − a² + b² c² = 2ab − 2ab + a² + b² a² + b² = c² (tw. Pitagorasa) Więc trójkąt jest prostokątny c.n.u. ufff + ab² + ac² + ba² + bc²

rumpek: Ostatnią końcówkę " + ab² + ac² + ba² + bc²" zapomniałem usunąć

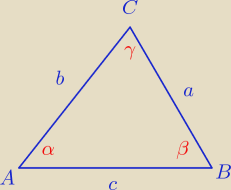
rumpek: Czas na zadanie 4, rysunek powyżej. Dowód zaraz powinien być

rumpek: Znowu korzystam z tw. cosinusów: T: 1 + cos²(α + β) = cos²α + cos²β 1^o a² = b² + c² − 2bccosα −2bccosα = a² − b² − c² / : (−2bc)

	a2 − b2 − c2
cosα =
	−2bc

2^o b² = a² + c² − 2accosβ −2accosβ = b² − a² − c² / : (−2ac)

	b2 − a2 − c2
cosβ =
	−2ac

3^o |∡C| = cos(180^o − (α + β) ) = −cos(α + β) c² = a² + b² + 2abcos(α + β) 2abcos(α + β) = c² − a² − b² / : 2ab

	c2 − a2 − b2
cos(α + β) =
	2ab

Podstawiając pod tezę zadania, otrzymamy: 1 + cos²(α + β) = cos²α + cos²β

	(c2 − a2 − b2)2		(a2 − b2 − c2)2
1 +		=		+
	4(ab)2		4(bc)2

(b2 − a2 − c2)2
4(ac)2

No i dalej tak idziemy jak w zadaniu 3 , co do obliczeń to nawet wolframaplha sie już zacina xD Z tego potem powinniśmy otrzymać tw. Pitagorasa . Się zastanawiam nad jednym − bo teoretycznie można by jeszcze to zadanie zrobić opierając się na samych kątach (bez tw. cosinusów).

Godzio: Kolo 22 sprawdze

rumpek: I jak sprawdzisz?

kylo1303: Ja od siebie powiem ze pierwsza 2 sa proste i masz je dobrze. A co do reszty to twoje rozwiazania skutecznie mnie zniechecily