... ICSP: Na czworokącie ABCD można opisać okrag. Niech P,Q,R i S będą rzuta,mi prostokątnymi punktu przecięcia przekątnych tego czworokąta na proste zawierające kolejne boki. Udowodnij że w czworokąt PQRS można wpisać w okrąg.

Vax: https://matematykaszkolna.pl/forum/118925.html

ICSP: a a myślałem że w czworokąt można wpisać w okrąg wtedy kiedy sumy jego przeciwległych boków są sobie równe. Nie pamiętam nic o dwusiecznych

Vax: Ale można też pokazać, że wszystkie dwusieczne danego czworokąta tną się w jednym punkcie, to jest równoważne (W końcu dwusieczna to prosta jednakowo oddalona od dwóch boków, jeżeli istnieje punkt przecięcia czterech dwusiecznych to jest to punkt jednakowo oddalony od wszystkich boków czyli środek okręgu wpisanego)

ICSP: oo ciekawe Tak samo można pokazać ze jeżeli 4 symetralne boków czworokąta przecinają się w jednym punkcie to ten punkt jest środkiem okręgu opisanego?

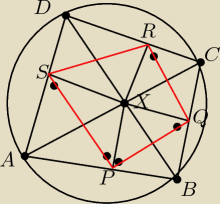
Vax: Tak, co do Twojego zadania to rozpiszę może rozwiązanie: Zauważmy, że na czworokącie PBQX da się opisać okrąg (sumy dwóch przeciwległych kątów sumują się do 180) więc <XPQ = <XBQ = <DBC, podobnie na czworokącie APXS da się pisać okrąg więc <XPS = <XAS = <CAD, ale jako kąty oparte na tych samych łukach <CAD = <DBC, więc <XPQ = <XPS czyli PX jest dwusieczną QPS, analogicznie dowodzimy, że <PSX = <XSR, <SRX = <XRQ , <RQX = <XQP, czyli punkt X jest punktem przecięcia dwusiecznych kątów czworokąta PQRS, więc jest środkiem okręgu wpisanego w dany czworokąt, więc istotnie w dany czworokąt da się wpisać okrąg, cnd.

Eta: No i ok dla Vax

Vax: O, dziękuję

ICSP: Zaraz to przenalizuję Na razie idę dowodzić twierdzenia cosinusów Jak ktoś chce mogę dać jakieś twierdzenie do dowodzenia bo mam kilka na jutro

Vax: Możesz napisać, ale jbc odpiszę dopiero po 22:30, czy 23 bo teraz muszę się nauczyć angielskiego na sprawdzian