???? kila: W trójkącie prostokątnym ABC poprowadzono odcinek DE równoległy do przeciwprostokątnej AB tak że D należy do BC i E należy do AC. Długość tego odcinka jest równa długości przyprostokątnej AC, kąt przeciwległy tej przyprostokątnej ma miarę alfa. Oblicz stosunek pola trójkąta DEC do pola trójkąta ABC.

kila: proszę pomóżcie

Eta:

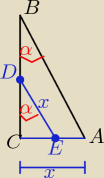
	|BC|
w ΔCAB		= ctgα ⇒ |BC|= x*ctgα
	x

	1		x2*ctgα
P(ΔABC)=		*x*|BC|=
	2		2

	|DC|
w ΔDEC		= cosα ⇒ |DC|=x*cosα
	x

	1		x2*cosα*sinα
P(ΔDEC)=		*x*|CD|*sinα =
	2		2

	PΔDEC		x2*cosα*sinα
to:		=		= ........ = sin2α
	PΔABC		x2*ctgα