planimetria Krystian: z przeciwleglych wierzcholkow prostokata poprowadzono odcinki prostopadle do przekatnej. Odcinki te dziela przekatna na 3 czesci po 8 cm. oblicz pole tego prostokata.

Basia: Zrób taki rysunek: ABCD − prostokąt AB = CD = a AD = BC = b AC − przekątna BB₁ prostopadły do AC DD₁ prostopadły do AC AD₁ = D₁B₁ = B₁C = 8 DD₁ = BB₁ = c (dlaczego ? zastatnów się) z trójkąta prostokątnego AD₁D mamy AD² = AD₁² + DD₁² b² = 8² + c² c² = b² − 8² −−−−−−−−−−−−−−−−−−−−−− z trójkąta prostokątnego AB₁B mamy AB² = AB₁² + BB₁² a² = 16² + c² c² = a² − 16² −−−−−−−−−−−−−−−−−−−−−−−−− a² − 16² = b² − 8² a² − b² = 16² − 8² −−−−−−−−−−−−−−−−−−−−−−−−− z trójkąta prostokątnego ABC AC² = AB² + BC² (3*8)² = a² + b² a² + b² = 9*8² −−−−−−−−−−−−−−−−−−−−−−−−−−−− a² − b² = 16² − 8² a² + b² = 9*8² −−−−−−−−−−−−−−−−−−−−−−−−−−− 2a² = 16² + 8*8² 2a² = (2*8)² + 8*8² 2a² = 4*8² + 8*8² 2a² = 12*8² a² = 6*8² a = √6*8² = 8√6 6*8² + b² = 9*8² b² = 9*8² − 6*8² b² = 3*8² b = √3*8² = 8√3 P = 8√6*8√3 = 64√18 = 64√9*2 = 64*3√2 = 192√2

Krystian: BB1 to mam poprowadzic z wierzcholka czy jak?

Basia: Oczywiście, że z wierzchołka B. A DD₁ z wierzchołka D.Tak jest w treści zadania.

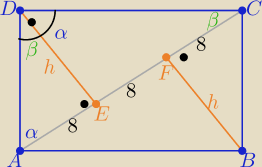
Eta: |AE|=8, |EC|=16 , |AC|=24 W ΔACD z podobieństwa trójkątów AED i DEC z cechy (kkk) :

	8		h
		=		⇒h2=8*16 ⇒ h=√64*2= 8√2
	h		16

P(ABCD)=h*|AC|= 8√2*24 P(ABCD)=192√2 cm² ===================

Eta: No to jeszcze długości boków i obwód : a=√16²+h²= √4*64+2*64=8√6 b=√8²+h²= √64+2*64= 8√3 Obwód L= 16√6+16√3= 16√3(√2+1) cm

Eta: Krystian już pewnie .... dzieci bawi

Mila: Myślę, że tak, ale ktoś odkopał zadanko.