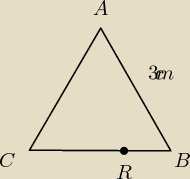 cześć mam takie zadanie. Trójkąt równoboczny ABC o boku = 3cm. Zginając kartkę w taki sposób,
że wierzchołek A znajduje się na boku CB tworząc punkt R IBRI = 13ICBI. Przecięcie tego
zagięcia z pozostałymi bokami tworzą punkty P i Q (P na odcinku IACI, Q na odcinku IABI.
Obliczyć odcinek IQRI trójkąta PQR.
Czy ktoś to potrafi?
cześć mam takie zadanie. Trójkąt równoboczny ABC o boku = 3cm. Zginając kartkę w taki sposób,
że wierzchołek A znajduje się na boku CB tworząc punkt R IBRI = 13ICBI. Przecięcie tego
zagięcia z pozostałymi bokami tworzą punkty P i Q (P na odcinku IACI, Q na odcinku IABI.
Obliczyć odcinek IQRI trójkąta PQR.
Czy ktoś to potrafi?
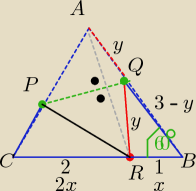 |RB|= 1 |CR|=2 ,bo |RB|+|CR|= x+2x=a= 3⇒ x=1
Punkty A i R są symetryczne względem prostej PQ ⇒ |QR|=|QA|= y
z tw. kosinusów w ΔBRQ wyznacz "y"
y2= 12+(3−y)2−2*1*(3−y)*cos60o
dokończ......
|RB|= 1 |CR|=2 ,bo |RB|+|CR|= x+2x=a= 3⇒ x=1
Punkty A i R są symetryczne względem prostej PQ ⇒ |QR|=|QA|= y
z tw. kosinusów w ΔBRQ wyznacz "y"
y2= 12+(3−y)2−2*1*(3−y)*cos60o
dokończ......