planimetria julka: W trapezie równoramiennym jedna z podstaw jest dwa razy dłuższa od drugiej, a przekątna jest dwusieczą kąta przy dłuższej podstawie. oblicz długości boków tego trapezu, wiedząc że jego pole równe jest 9. Oblicz także pole koła opisanego na tym trapezie.

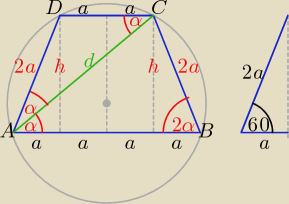
Bogdan: h = √(2a)² − a² = a√3

	1		1
Pole trapezu PABCD =		*7a*h = 9 ⇒		*7a*a√3 = 9 ⇒ a = ...
	2		2

	1
Pole trójkąta ABC PABC =		*4a * h = ...
	2

d = √(3a)² + h² = ... Okrąg o promieniu R opisany na trapezie ABCD jest jednocześnie okręgiem opisanym na trójkącie ABC

	4a * 2a * d
PABC =		⇒ R = ...
	4R

	d
R można także wyznaczyć z twierdzenia sinusów: R =		.
	2sin2α

Dość łatwo jest wykazać, że kąt wewnętrzny trapezu przy dolnej podstawie ma miarę 60^o, czyli 2α = 60^o. Pole koła P = πR² = ...