wyznacz dziedzinę funkcji. Łukasz:

	1
√x3−5x2−6x+
	√x2−7x

dzieląc pierwszy pierwiastek x³−5x²−6x przez (x−1) otrzymuję cos takiego: x²−4x−2, po wymnożeniu (x²−4x−2) (x−1) otrzymuję ( x³−5x²−6x+2) co źle robię?

Artur z miasta Neptuna: a po co dzielisz przez (x−1)? Ten wielomian nie dzieli się (bez reszty) przez (x−1). Ponieważ: x³ − 5x²−6x = x*(x² − 5x − 6) = x*(x−2)*(x−3).

Łukasz: (x2 − 5x − 6) w jaki sposób to rozłożyłeś w taką postać? (x−2)*(x−3) mi miejsca zerowe wychodzą x₁=1 i x₂=6.

Artur z miasta Neptuna: aaa sorki − w pamięci rozkładałem. Ale Ty masz złe miejsca zerowe. Powinny być jaki już x₁ = −1, x₂ = 6 ... ze wzrorów viete'a masz że x₁*x₂ = ^c_a = −6

Łukasz: no przepraszam, x₁=−1, zgadza się. to ten wielomian zzeruje się poprzez 6?

Artur z miasta Neptuna: tak ... zeruje się w x = 0 ∧ x = −1 ∧ x = 6. Więc pierwszy pierwiastek jest ≥0 w przedziałach <−1 ; 0>∪ <6 ; +∞). Z drugiego natomiast masz, że x∊(0:7). Więc dzieciną będzie D= <6,7).

Artur z miasta Neptuna: tfuuu ... oczywiście źle drugi pierwiastek napisałem ... x∊(−∞,0)∪(7; +∞). D_f = <−1 ; 0)∪ (7 ; +∞)

Łukasz: a możesz mi wytłumaczyć dlaczego: <−1 ; 0> to jest pierwszy przedział? bo siedzę i się głowię.

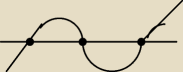
Artur z miasta Neptuna: dlatego: http://www.wolframalpha.com/input/?i=plot+x3+%E2%88%92+5x2%E2%88%926x+from+-2+to+7 masz trzy miejsca zerowe: (−1, 0, 6) i wszystkie są "pojedynczymi" miejscami zerowymi. Współczynnik "a" (przy najwyższej potędze) jest >0 więc, szkic wykresu zaczynasz rysować (zawsze zaczynasz od prawej strony) OD GÓRY i lecisz do miejsc zerowych. If miejsce zerowe jest nieparzystego stopnia to linia "przechodzi" przez oś else (czyli jak jest parzystego, np. dla wielomianu (x−2)²*(x−3), będzie dla x = 2) linia "odbija się od osi i hiperbolą leci do następnego miejsca zerowego.

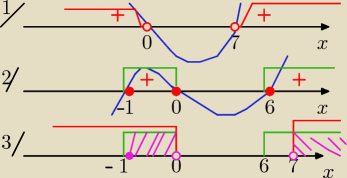
Eta: D: x² −7x >0 i x³−5x²−6x≥0 1/ x(x−7) >0 ⇔ x∊ (−∞, 0) U (7,∞) 2/ x(x−6)(x+1)≥0 ⇔x∊ <−1, 0> U <6,∞) 3/ jako odp. wybierasz część wspólną 1/ i 2/ D= <−1,0) U (7,∞)