Translacja o wektor F3CB1: Dana jest prosta k o równaniu y=2x−3. Znajdź równanie prostej m będącej obrazem prostej k o przekształceniu: a) T_[−³2,0] b) T_[0,3] c) T_[−2,1] d) T_[3,−3] Próbowałem sam robić to zadanie kilkukrotnie, lecz bezskutecznie. Prosiłbym o jakieś objaśnienia a propo tego zadania, bo niestety nic z tego nie rozumiem, tzn. wiem tylko tyle, że jest to przesunięcie wektora, ale nie potrafię wyliczyć tego przesunięcia. Będę wdzięczny za pomoc. Z góry dziękuję

F3CB1: Podbijam, bo jest to dla mnie bardzo ważne, a chciałbym to zrozumieć. Wierzę w was

beti: jeśli f. podst. ma wzór y=f(x), to przesuwając jej wykres o wektor [p,q] otrzymujemy równanie: y=f(x−p) + q Czyli:

	3
a)p=		, q=0
	2

	3
y = 2(x−		) −3 = 2x −3−3 = 2x−6
	2

b) p=0, q=3 y = 2x−3+3 = 2x c) i d) podobnie

F3CB1: Wielkie dzięki beti Nareszcie ktoś wytłumaczył mi to w sposób krótki i zwięzły. Jeszcze raz dzięki!

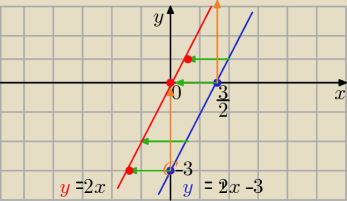
Eta: Wektor translacji T → u[a,b] to y= f(x−a)+b

	3
a) u=[−		, 0]
	2

	3
y= [2(x+		) −3] +0 ⇒ y= 2x+3 −3 ⇒ y= 2x co widzisz na wykresie
	2

po przesunięciu w lewo o 1,5 jednostki b) u=[ 0,3] y= [2(x−0) −3]+3 ⇒ y= 2x−3 +3 ⇒ y= 2x po przesunięciu w górę o 3 jednostki c) u=[−2,1] y= 2(x+2)−3] +1 ⇒ y=.... po przesunięciu w lewo o 2 jednostki i w górę o 1 jednostkę d) napisz sam ......

Eta: @beti w a) coś nie tak ? pozdrawiam

beti:

	3
p jest niewyraźnie napisane −− ja przyjęłam, że p =
	2

Eta: Ja wiem,że ty to wiesz Czy zainteresowany będzie wiedzieć? (dlatego napisałam )

beti: oto jest pytanie ....

Eta: Ty oczywiście (sorry

F3CB1: Eta, to wyjaśnienie jest świetne! Wielkie dzięki Beti, w a) było −³₂, ale poprawiłem i jest dobrze Uff, ale mi ulżyło