trygonometria Hashiri: Witam, Mam takie zadanie:

	1
Wiedzac, ze sinα−cosα=		i α<90stopni oblicz sinα+cosα=
	4

Proszę o szybka pomoc.

ICSP:

	1		1		15
sinα − cosα =		⇔ 1 − 2sinαcosα =		⇔ 2sinαcosα =
	4		16		16

(sinα + cosα)² = 1 + 2sinαcosα

	31
(sinα + cosα)2 =
	16

	√31
sinα + cosα =		dziwny wynik. Sprawdź obliczenia.
	4

V.Abel: spróbuj cos α zamienić na sin(90−α) a potem wykorzystaj wzór na różnicę sinusów tj. sinα−sinβ=2sin(α+β)/2 * cos(α−β)/2 powodzenia !

Hashiri: Dzięki masz rację >

Hashiri: Mam jeszcze takie dziwne, ale w ogóle nie wiem jak taka funkcja wygląda, choć znam zasady przekształceń wykresów: ZAD: Jaka jest dziedzina i wzór takie funkcji tryg. :

	|sinx|
f(x) =		?
	sinx

ICSP: D : sinx ≠ 0 f(x) : 1 dla sinx> 0 −1 dla sinx < 0

V.Abel: w sumie, to ICSp ma rację, bo po głębszej analizie treści najpierw obliczasz wartość wyrażenia sinα−cosα= 1/4 potem dopiero możesz ze wzoru na sumę sinusów // Przeprawszam, zbyt szybko udzieliłem odpowiedzi, nie czytając do końca treści

Hashiri: hmm.. nie rozumiem dlaczego

V.Abel: Chcąc rozwiązać równanie trygonometryczne dążysz do wyliczenia kątów, jeśli zrobisz tak jak powiedziałem na początku, to właśnie wyjdą Ci kąty, które ani jak mają się do dalszej części zadania, tj sinα+cosα=... // tzn. musisz to zrobić właśnie tak jak zrobił to ICSP // z czasem nabierzesz wprawy,

Hashiri: Tak, tamto już wiem, tylko chodzi mi z ta nowa funkcja co potem napisalem f(x) [post 15 sty 17:09] Nie rozumiem co z tym zrobił ICSP, ze takie wyniki mu wyszły i poprosiłbym jak w ogóle ta wunkcja przebiega, bo w ogóle jej nie moge se jej wyobrazić

ICSP: rozwiązuj te równania i nierówności. Otrzymasz przedziały. Później wystarczy tylko narysować ładny wykres.

ICSP: dobrze wyjaśnię jeszcze raz :

	|sinx|
f(x) =
	sinx

najpierw dziedzina: Mianownik musi być różny od 0 czyli sinx ≠ 0 rozwiąż równanie : sinx = 0 To jest pierwszy krok.

Hashiri: a dalej ?

ICSP: no czekam na ciebie. Masz rozwiązać takie równanie. Przecież nie zrobię za ciebie całego zadania No chyba że znasz metodę itteracjną to się jakoś dogadamy

Hashiri: x=0 stopni

ICSP: ty jesteś na podstawie czy na rozszerzeniu?

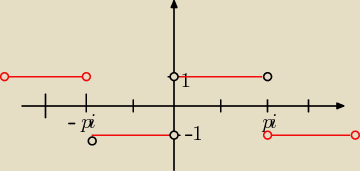
Aga: f(x)=1, gdy sinx>0 f(x)=−1, gdy sinx<0

Hashiri: A mogłby ktos zrobic szybki rysunek Prosze

Aga: