Prosze o sprawdzenie:* Iza: Proszę o sprawdzenie! Niech A,B oznaczają zdarzenia zawarte w przestrzeni zdarzeń elementarnych Ω. Wiadomo, że P(A')= 0,37 P(B)= 0,32 P(A−B)= 0,43. Oblicz P(A∩B) i P(A∪B). P(A)= 1−P(A') P(A)= 0,63 0,43= 0,32−P(A∩B) P(A∩B)= −0,11 P(A∪B)= 0,63+ 0,32+ 0,11 P(A∪B)=1,06

Andrzej: o matko jedyna... prawdopodobieństwo musi się zawierać w przedziale <0,1>, więc nie ma takiego cudu żeby wyszło −0,11 ani 1,06...

Iza: Czyli jak to rozwiązać?

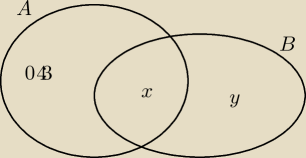
Andrzej: x+y=0,32 0,43+x=0,63

Andrzej: gdzie x oznacza P(A∩B) y oznacza P(B−A) a 0,43 to P(A−B)

Iza: Czyli P(A∪B)= 0,75. Bardzo dziękuje za pomoc!