funkcja kwadratowa, oś symetrii eureka: Wyznacz równanie osi symetrii wykresów poniższych funkcji kwadratowych: a)f(x)=x²−x−6 b)f(x)=−x²+6x−8 Narysowałam oba wykresy, tylko jak teraz ustalić i wyznaczyć równanie osi symetrii?

Kejt: ma je na pewno.. musisz policzyć jedną ze współrzędnych wierzchołka..y=p

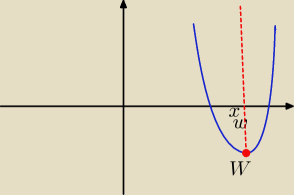
Patronus: oś symetrii paraboli to prosta x=p, gdzie "p" to współrzędna iksowa wierzchołka.

	1
a) x=
	2

b) x=3

Eta:

	−b
osią symetrii paraboli jest prosta o równaniu : x= xw=
	2a

	1
a) xw=
	2

	1
osią symetrii jest prosta o równaniu x=
	2

darel: y=x²−16

bezendu: i co z tym trzeba zrobić y=(x−4)(x+4)

Weronika: y=(x−4)(x+4) trzeba znaleźć miejsca zerowe tzn X a zrobić trzeba tak: x−4=0 x=4 x+4=0 x=−4 zrobić wykres −> zaznaczyć −4 i 4 i punktem przecięcia osi symetrii będzie 0.

wico:

sara: f(x)=2(x+4)²

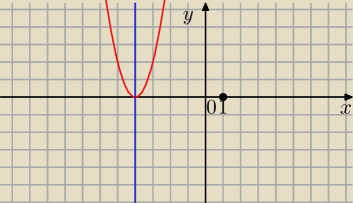
janek191: f(x) = a*(x − p)² + q mamy f(x) = 2*( x + 4)² p = −4 Oś symetrii x = p Odp. x = − 4 ========= Patrz też na wykres