uzasadnij, że 61^16<18^24 Daria: uzasadnij, że 61¹⁶<18²⁴

Aga: 16=8*2 24=8*3 (61)¹⁶=((61)²)⁸ 18²⁴=(18³)⁸ Z dwóch potęg o jednakowych wykładnikach ta jest większa, której podstawa jest większa.

TOmek: ja to zrobiłem tak 81¹⁶>61¹⁶ (dałem tu wytlumaczenie chociaz to logiczne) sprawdzam co jak działa nierównosc dla wypadku 81¹⁶<18²⁴ 3⁶⁴<3⁹⁶ 64<96 nierównosc prawdziwa czyli 61¹⁶<81¹⁶<18²⁴ co udowadnia nam nierówność 61¹⁶<18²⁴

TOmek: ciekawe czy moje rozumowanie będzie zaliczone .. <hmm>

Eta: 61¹⁶ < 64¹⁶ <18²⁴ 64¹⁶= (4³)¹⁶= 4⁴⁸= (4²)²⁴ = 16²⁴ zatem 16²⁴< 18²⁴ c.n.u.

TOmek: Eta jak myslisz, moje rozumowanie chyba tez jest ok?

Eta: też ok

TOmek: Tego zadania prawie w ogole nie ruszyłem: Na bokach AC i BC trójkąta obrano punkty P i Q takie ,ze |AP| : |PC|=2:1 oraz |BQ| : |QC|=2:1. Odcinki AQ i BP przecinają sie w punkcie R. Wykaż ,ze pole czworokątna CPRQ jest równe polu trójkąta ARP. −−− byłbym wdzieczny gdyby ktos zrobił

Daria: Teraz to na prawdę oczywiste : D Dziękuję bardzo, nie wiedziałam jestem w 2. klasie szkoły średniej i właśnie robię maturę rozszerzoną z matmy, z tym miałam problem : ) Ta strona jest genialna

TOmek: tyko z tym zadaniem miałas problem?

Daria: Nie skończyłam, ale jak będę miała problem z jakimś innym, to chyba mogę liczyć na pomoc? : )

BLAZEJ_505: a ten dowód to najlepiej zrobić metodą nie wprost Teza: 61¹⁶<18²⁴ Dowód nie wprost: załóżmy że teza jest fałszywa,czyli 61¹⁶>18²⁴, zatem (61²)⁸>(24³)⁸ obustronnie pierwiastkujemy pierwiastkiem 8 stopnia I61²I>I24³I opuszczamy wartości bezwzględne bo pod nimi są wartości dodatnie 61²>24³ 3 721>13 824, co jest sprzecznością, zatem 61¹⁶<18²⁴ jest prawdziwe. Co należało uzasadnić

Daria: Nie skończyłam, ale jak będę miała problem z jakimś innym, to chyba mogę liczyć na pomoc? : )

TOmek: taaa

Eta:

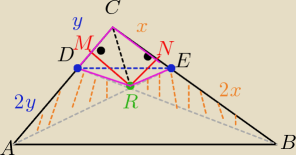
Eta: Ja to widzę tak:

	1
Δ DCE ~ ΔABC w skali k=		⇒ że czworokąt ABDE jest trapezem AB || DE
	3

zatem pola ΔARD i ΔBRE są równe ( znane twierdzenie .... RM jest wspólną wysokością trójkątów ARD i RCD oraz RE jest wspólną wysokością trójkątów BRE i RCE

	1
P ΔRCD=		PΔARD
	2

	1
i P ΔRCE =		PΔBRE i PΔARD=PΔBRE
	2

−−−−−−−−−−−−−−−−−−−−−−−−− dodając stronami: P(CRDE) = PΔARD c.n.u Sorry zamiast oznaczeń P i Q napisało mi się na rys. E i D

kylo1303: Tomek Apropo twojego rozumowania w zadaniu z potegami: Skad ci sie wzielo 3⁹⁶? Bo jesli z 18²⁴ to jest to blad i twoje rozumowanie nie jest dobre. Ewentualnie ja cos pominalem.

Eta:

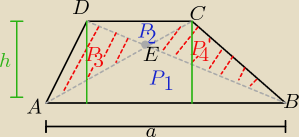
	a*h		a*h
PΔABD = P1+P3 =		i PΔABC= P1+P4=
	2		2

zatem : P₁+P₃= P₁+P₄ ⇒ P₃= P₄

TOmek: no tak skopałem...

TOmek: dziekuje Eto

Eta: To po co "kopałeś"