F. kwadratowa Danieloo: Zad 1 Zapisz wzór funkcji f, która każdej liczne n∊N+ przyporządkowuje największą liczbę całkowitą x spełniającą nierówność x² − 2nx − 8n² < 0. Zad 2 Dla jakich wartości parametru m równanie x² + (m−1)x + m − 2 = 0 ma dwa różne pierwiastki, z których jeden jest sinusem, a drugi cosinusem tego samego kąta? Tak wpadłem na założenia, że Δ > 0 i to obliczyłem i jeszcze do tego stwierdziłem, że c = m − 2 = sinxcosx i −b = 1 −m = sinx + cosx i stanąłem bo nie wiem co dalej...

ICSP: x₁ = sinus kąta x₂ = cosinus kata z jedynki trygonometrycznej : x₁² + x₂² = 1 x₁² + x₂² = (x₁ + x₂)² − 2x₁x₂

Alkain: zad.1 funkcja ma przyporządkowywać największą liczbę całkowitą ale mniejszą od miejsc zerowych więc: Δ=4n²+4*1*8n² √Δ=6n

	2n+6n
x1=		=4n
	2

	2n−6n
x2=		=−2n
	2

f(n)=4n nasza funkcja ale musi wyznaczać najwyższą możliwą i x² − 2nx − 8n² < 0 czyli wzór funkcji f(n)=4n−1

Danieloo: O ja... źle policzyłem pierwiastki w tym pierwszym hehe, ale wielkie dzięki

kaaro: dlaczego jst 4n − 1 ?

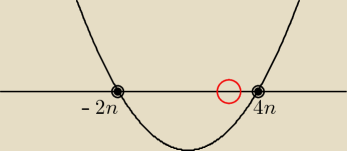
BorowikSzlachetny: 4n−1 ponieważ jak narysujesz sobie wykresik to będzie on wyglądał jakoś tak jak na rysunku moim. Nierówność jest skierowana jest na "poniżej zera" więc szukamy liczby całkowitej największej, ale wciąż będącej w "ramach" nierówności. Dlaczego nie 4n? Bo nierówność jest < a nie ≤, więc musimy odrzucić wartość krańcową

meg: a dlaczego f= 4n ?