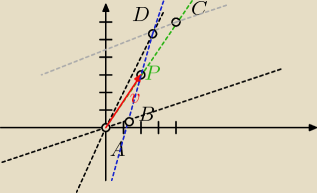
 równania 2x−y = 0 i x − 3y = 0 są to równania ogólne prostych, przekształcamy je na równania
kierunkowe i otrzymujemy
y = 2x i y = 13x równania te mają współczynniki kierunkowe a równe
a = 2 i a = 13 nie są one jednakowe co oznacza, że proste nie są równoległe więc są
to proste przecinające się, czyli wychodzące z jednego wierzchołka.
Przyrównujemy te równania i otrzymujemy punkt A przecięcia się prostych
A(0,0)
Teraz wyznaczamy wspórzędne wektora v
a = xP−xA = 2−0 = 2
b = yP−yA = 3−0 = 3
Mamy wektor o współrzędnych [2,3]
ponieważ przekątne równoległoboku dzielą się na połowy, to po pomnożeniu wektora przez 2
otrzymamy współrzędne wektora AC→ [4,6]
[4,6] = [xC−xA , yC−yA]
stąd obliczymy wspólrzędne punktu C(4,6)
przez punkt C przecodzi prosta równoległa do prostej y = 13x więc jej równanie wynosi
y = 13(x−4)+6 = 13x + 143
porównując tę prostą z prostą y = 2x otrzymamy punkt D (145 ,285)
teraz możemy policzyć równania przekatnych jako przechodzących przez 2 punkty
jedna przez punkty A(0,0) i P(2,3) , druga przez punkty D(145, 285) i P(2,3)
równania 2x−y = 0 i x − 3y = 0 są to równania ogólne prostych, przekształcamy je na równania
kierunkowe i otrzymujemy
y = 2x i y = 13x równania te mają współczynniki kierunkowe a równe
a = 2 i a = 13 nie są one jednakowe co oznacza, że proste nie są równoległe więc są
to proste przecinające się, czyli wychodzące z jednego wierzchołka.
Przyrównujemy te równania i otrzymujemy punkt A przecięcia się prostych
A(0,0)
Teraz wyznaczamy wspórzędne wektora v
a = xP−xA = 2−0 = 2
b = yP−yA = 3−0 = 3
Mamy wektor o współrzędnych [2,3]
ponieważ przekątne równoległoboku dzielą się na połowy, to po pomnożeniu wektora przez 2
otrzymamy współrzędne wektora AC→ [4,6]
[4,6] = [xC−xA , yC−yA]
stąd obliczymy wspólrzędne punktu C(4,6)
przez punkt C przecodzi prosta równoległa do prostej y = 13x więc jej równanie wynosi
y = 13(x−4)+6 = 13x + 143
porównując tę prostą z prostą y = 2x otrzymamy punkt D (145 ,285)
teraz możemy policzyć równania przekatnych jako przechodzących przez 2 punkty
jedna przez punkty A(0,0) i P(2,3) , druga przez punkty D(145, 285) i P(2,3)
| 0+xC | 0+yC | ||
=2 i | =3 | ||
| 2 | 2 |